|
7 - Permutazioni con ripetizione assegnata.
Abbiamo già visto un esempio di permutazioni nella composizione di tutti i possibili anagrammi di una parola. Le permutazioni semplici comportano una limitazione implicita: le parole devono avere tutte lettere differenti, dal momento che uno stesso elemento non può essere ripetuto più volte. Proviamo, invece, ad anagrammare la parola MAMMA, in cui compaiono tre M e due A. La situazione si complica, poiché, mentre uno scambio tra la 2 a e la 3 a lettera darebbe luogo alla nuova parola MMAMA, uno scambio tra la 1a e la 3 a o tra la 1 a e la 4 a darebbe luogo sempre alla stessa parola MAMMA.
La formula che determina il numero di permutazioni di k elementi, il primo ripetuto k1 volte, il secondo k2 volte, l'ennesimo ripetuto kn volte, ponendo n = (k1 + k2 + ... + kn), è dunque: 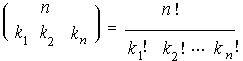 Il simbolo a sinistra della formula, in analogia con quanto fatto per le combinazioni (il cui simbolo è stato chiamato coefficiente binomiale), è denominato coefficiente multinomiale. Usando la suddetta formula, si possono calcolare tutti gli anagrammi della nota espressione siciliana "QUAQUARAQUA" che sono ben 277.200. |