|
8 - Combinazioni con ripetizione.
Abbiamo già visto la differenza essenziale tra disposizioni e combinazioni semplici. Essa consiste nel fatto che queste ultime non considerano l'ordine con cui sono elencati gli elementi in un raggruppamento, quale motivo di distinzione tra l'uno e l'altro.
Anche tra disposizioni e combinazioni con ripetizione permane la stessa differenza, già vista per quelle semplici. Le parole AABBB e BABAB, formate da due A e tre B, in ordine differente sono considerate due diverse disposizioni, mentre le stesse costituiscono una sola combinazione, essendo indifferente l'ordine con cui compaiono gli elementi.
Il principio del pastore consente di passare dalle disposizioni semplici alle combinazioni semplici, eliminando tutte le disposizioni costituite dallo stesso insieme di elementi, scritti in ordine differente.
Nel caso delle disposizioni e combinazioni con ripetizione, la situazione si complica un po'. La ripetizione, non prefissata, degli stessi elementi fa variare il numero delle ripetizioni stesse. Sono infatti disposizioni diverse AABBC e AABBB. La prima dà luogo, permutando i vari elementi, a 30 diverse parole, che corrispondono ad una stessa combinazione. La seconda ne produce, invece, solo 10, con gli stessi elementi in ordine differente. Il principio di divisione ci porterebbe a dividere ogni volta per un valore variabile (il primo gruppo per 30 ed il secondo per 10) e così via.
Con pochi elementi, con un po' di pazienza, sarebbe possibile costruire tutte le possibili disposizioni e poi eliminare quelle che producono combinazioni equivalenti. Tale procedura finirebbe tuttavia per diventare troppo laboriosa con un numero di elementi appena un po' numeroso. Occorre perciò cercare altre vie per ottenere il risultato.
Osserviamo, intanto che le combinazioni semplici di n elementi di classe k sono sempre in corrispondenza biunivoca con le permutazioni di due elementi, il primo ripetuto k volte e il secondo ripetuto (n-k) volte; si ha infatti, rispettivamente:
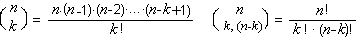
Basta infatti moltiplicare i due termini della prima frazione per (n-k)! e si ottiene immediatamente la seconda formula.
| Dimostriamo ora che la corrispondenza tra combinazioni e permutazioni di due elementi, il primo ripetuto k volte ed il secondo (n-k) volte, vale anche per il caso delle combinazioni con ripetizione.
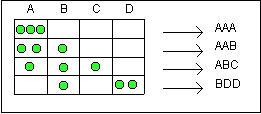
Usiamo un modello frequente in combinatoria: quello delle biglie e delle scatole. Una combinazione è indicata da un numero n di scatole, contraddistinte ciascuna da una lettera. Si prendono k biglie e si dispongono nelle n scatole; trattandosi di combinazioni con ripetizione, una scatola potrà contenere da 0 a k biglie. La biglia indicherà quale scatola sarà considerata di volta in volta. Vediamo alcuni esempi nello schema qui a lato. |
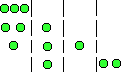
| Consideriamo la situazione appena descritta da un altro punto di vista. Togliendo la cornice esterna e le pareti divisorie orizzontali dallo schema precedente, rimane una successione di biglie e di pareti divisorie verticali che dividevano una scatola dall'altra. Nello schema a lato, su ogni riga, sono presenti tre biglie e tre pareti divisorie. Le varie combinazioni si ottengono permutando in vari modi le tre biglie e le tre pareti divisorie (barrette).
Ciò corrisponde a trovare tutti gli anagrammi della parola AAABBB, in cui la A rappresenta le biglie e la B le barrette. |
Non è difficile allora vedere la corrispondenza tra le combinazioni con ripetizione di tre lettere, prese da un alfabeto di 4 lettere, e le permutazioni di 6 elementi (biglie + barrette), il primo (biglie) ripetuto 3 volte e il secondo (barrette) ripetuto (6 - 3) volte. Generalizzando, se si hanno n scatole e k biglie, le combinazioni con ripetizione di n elementi di classe k, corrisponderanno alle permutazioni di due elementi il primo ripetuto k volte ed il secondo (n-1) volte. Avremo la seguente formula:
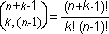
Tale formula, che fornisce il numero di combinazioni con ripetizione di n elementi di classe k, può essere scritta in altro modo, dividendo i due termini della frazione per (n-1)! :

Si calcola cioè il fattoriale crescente di k fattori a partire da n e si divide per k! . Tale formula, applicata al caso delle 4 scatole e 3 biglie, darà:

|

