3 - Permutazioni semplici.

Si definiscono permutazioni semplici quelle particolari combinazioni per le quali valgono le seguenti regole:

• abbiamo a disposizione n oggetti, tutti differenti;
• formiamo le varie combinazioni usando ogni volta tutti gli oggetti , ciascuno preso una sola volta;
• una combinazione differisce da un'altra per l'ordine in cui gli oggetti sono disposti.

Il termine "semplici" (che incontreremo anche più avanti) sta ad indicare la regola per la quale non si possono ripetere gli stessi elementi all'interno di ogni permutazione.
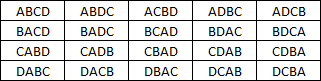
Ad esempio, dato un alfabeto formato dalla lettere {A,B,C,D}, formare tutte le possibili parole di quattro lettere, senza ripetere nessuna di esse. Dovendo usare ogni volta tutte le lettere disponibili, l'unica operazione consentita è quella di scambiarle di posto, anagrammando la parola. Quante diverse parole si possono ottenere?
L'uso di grafi ad albero può aiutarci a trovare la risposta. Si parte dal primo nodo in alto e si tracciano quattro rami per indicare l'iniziale della parola, che può essere una delle quattro lettere A, B, C, D. Ognuno dei quattro rami genera a sua volta tre rami, per indicare ciascuna delle lettere rimaste, da scrivere al secondo posto. Sistemate le prime due lettere, andiamo a sistemare la terza: sarà una delle due indicate su ciascuno dei due rami che seguono. Si arriva così all'ultima ramificazione con un solo ramo, che indica la quarta ed ultima lettera rimasta.

Per avere tutte le permutazioni, basterà partire dal vertice sulla sommità dell'albero e scrivere di seguito tutte le lettere che s'incontrano lungo il percorso che conduce a ciascuno dei rami terminali. Si ottengono in tal modo tutte le permutazioni indicate nella tabella a lato. Quante ne sono? Il conto è facile: 24.

Osserviamo che tale numero si ottiene contando i vari rami generati dall'albero. I quattro rami iniziali generano tre rami, ciascuno dei quali ne produce due, che ne producono infine ancora un altro. Basta moltiplicare 4 × 3 × 2 × 1 e si ottiene 24.
Proviamo ora a generalizare il procedimento. Se, anziché 4 lettere, ne avessimo avute 5, 6 o n, i rami iniziali sarebbero stati rispettivamente 5, 6, n, per poi decrescere fino ad arrivare al ramo terminale. Avremmo dovuto calcolare il prodotto di 5, 6, n fattori decrescenti fino ad 1. Abbiamo così scoperto il fondamentale principio di moltiplicazione, in base al quale si risolvono molti problemi di tipo combinatorio. In matematica, il prodotto di n fattori interi decrescenti da n ad 1 si chiama fattoriale di n e si indica con il simbolo n! (si legge n fattoriale), che è anche il simbolo con cui si indicano le permutazioni semplici di n oggetti:

n! = n∙ (n-1)∙ (n-2) ∙ (n-3)....3∙ 2 ∙1

Il punto esclamativo è dovuto al senso di meraviglia che suscita il rapido crescere di n! al crescere di n. Vediamo alcuni valori, calcolati tenendo presente che n! = n.(n-1)! e che, per convenzione si pone 0! = 1 (del resto, c'è un solo modo di scrivere una parola usando zero caratteri: non scrivere nulla!).

n	0	1	2	3	4	5	6	7	8	9	10
n!	1	1	2	6	24	120	720	5.040	40.320	36.2880	3.628.800

Si vede che già con 10!, si ottiene un valore di oltre 3 milioni e mezzo. Basta un numero non troppo grande, per avere fattoriali di valore impressionante. Ad esempio, utilizzando tutte le 21 lettere dell'alfabeto italiano, gli anagrammi di 21 lettere sono:
21! = 51.090.942.171.709.440.000 » (5.11 x 10¹⁹)

E' perfino difficile leggere un numero così grande: sono oltre 51 miliardi di miliardi. Scrivendo una parola al secondo, ci vorrebbero 1.620.083.148.519 anni per scriverle tutte, più dell'età stimata dell'universo. Gli inglesi, che usano un alfabeto di 26 caratteri, impiegherebbero ancora di più per scrivere tutti i 403 milioni di miliardi di miliardi e passa di parole che si possono ottenere anagrammando il loro alfabeto.