1 – Le regole del gioco. Il futoshiki è un gioco di origine giapponese che, si va diffondendo in molti altri Paesi sulla scia del più noto sudoku. Si presenta come uno schema di caselle disposte in forma di quadrato. Qui a lato vediamo un esempio di schema a 25 caselle divise in 5 righe e 5 colonne. Vi sono futoshiki da 36 caselle (6 ´ 6) o da 49 caselle (7 ´ 7). Alcune celle hanno già inserita una cifra, che non può essere cambiata. Scopo del gioco è di completare lo schema, riempiendo tutte le celle, con cifre da 1 a 5, o da 1 a 6, o da 1 a 7, a seconda delle dimensioni dello schema.

2 – Sequenze ordinate. Oltre ai termini usati nel già citato articolo sul sudoku (solitari, doppiette, triplette) , introduciamo la nuova definizione di sequenza ordinata, intesa come un successione continua di celle legate tra loro da uno stesso segno di ordinamento. In pratica, le freccette che collegano le varie celle della sequenza sono tutte orientate nello stesso verso. Le celle della sequenza possono appartenere tutte ad una stessa riga (celle verdi) o ad una stessa colonna (celle gialle), ma possono anche iniziare da una riga e poi "svoltare" su una colonna (vedi celle rosse) o viceversa. Si possono avere anche sequenze che procedono zigzagando lungo un percorso continuo tra righe e colonne. Una sequenza minima è formata da due sole celle con un segno di ordinamento tra di esse ( celle lilla).

Una sequenza massima si avrebbe nel caso di un numero di celle ordinate pari al valore massimo (rango) dello schema (6 nel nostro esempio), tutte collegate da freccette orientate nello stesso verso, ma è un caso piuttosto raro poiché per tali celle sarebbe già pronta la soluzione: tutti i numeri da 1 in poi, in sequenza, nelle varie celle.

3 – Strategie di gioco.
Come per il sudoku, è consigliabile usare i margini bianchi attorno allo schema per scrivere l'elenco dei numeri mancanti da inserire nelle celle vuote di ciascuna riga o colonna, facilitando la ricerca delle possibili soluzioni. In base ad esse, inseriremo a matita i candidati in ciascuna cella vuota dello schema. Una volta trovata la soluzione per una delle celle, la scriveremo col pennarello, cancellando ogni traccia dei precedenti candidati. Saranno parimenti ridotti i candidati elencati a margine dello schema, in corrispondenza della soluzione trovata.
Alcune soluzioni sono di immediata evidenza: supponiamo ad esempio che si debba trovare una cifra minore di 2: c'è solo la cifra 1 che soddisfa la richiesta. In un futoshiki di rango 7   s'impone di trovare un numero maggiore di quello della cella a fianco, che contiene il 6,: è ovvio che la soluzione è proprio il 7, l'unica cifra disponibile maggiore di 6.
Come per il sudoku, sarebbe preferibile in genere rivolgere la nostra attenzione alle righe o alle colonne con il maggior numero di celle già definite, dovendo analizzare  un minor numero di cifre da candidare nelle celle ancora vuote. Per il futoshiki, tuttavia, è preferibile partire dalla sequenze ordinate descritte nel paragrafo precedente.
 
4 – I candidati nelle sequenze ordinate.
Si parte dalle sequenze ordinate più lunghe per poi proseguire in quelle via via più corte. Le cifre da candidare nelle varie celle della sequenza obbediscono ad una regola: esse formano altrettante serie ordinate, la cui lunghezza dipende dal numero di celle che costituiscono l'intera sequenza. Detto m il valore della massima cifra e s il numero di celle della sequenza ordinata, il numero di cifre che si possono candidare il ciascuna cella delle sequenza stessa sarà dato dal valore di (m-s+1). E' bene chiarire il concetto con un esempio. Supponiamo di dover completare uno schema di 6 ´ 6 caselle e di aver individuato una sequenza ordinata di 4 celle. In ogni cella avremo una sequenza lunga (6-4+1), cioè con 3 cifre candidabili. La prima cella avrà una serie che va da 1 a 3.  Le altre celle a seguire saranno formate da serie in cui il primo e l'ultimo termine sono aumentati di una unità rispetto alla serie precedente:  nella , seconda e terza e quarta cella scriveremo pertanto (2 3 4) ( 3 4 5) e (4 5 6). Ecco come si presenteranno le quattro celle della nostra sequenza ordinata:

5 - Una ... reazione a catena.
Il lavoro appena eseguito non è ancora terminato. Occorrerà infatti esaminare una alla volta le varie celle della sequenza, eliminando da ciascuna di esse le cifre eventualmente già presenti nella stessa riga o colonna. La regola è infatti quella di non usare nessuna cifra più di una volta in una stessa riga o in una stessa colonna e quindi è inutile candidarne una già presente. Possiamo così restringere il numero di candidati in qualcuna delle celle. Il processo di eliminazione di numeri doppioni cambia se ad essere interessato è il termine massimo o il termine minimo di una delle celle della sequenza: nel primo caso occorrerà eliminare il termine massimo anche in tutte le altre celle precedenti a quella in cui è avvenuta la prima eliminazione; nel secondo caso dovremo eliminare anche il termine minimo in tutte le altre celle della sequenza successive a quella in cui è avvenuta la prima eliminazione. Supponendo che in una cella allineata con quella contenente i numeri 1 2 3 sia già presente il numero 1: dovremo togliere 1 dalla prima cella, in cui resteranno solo (2 3), ma, a seguire, dovremo togliere il termine minimo anche nelle successive celle della sequenza, nelle quali resteranno (3 4), (4 5) e (5 6).
Al contrario, se fosse presente un 6 in una cella allineata con l'ultima della nostra sequenza, oltre che togliere da essa il 6, dovremmo togliere a ritroso anche il termine più alto nelle altre celle della sequenza, che risulterà infine formata dai seguenti termini: (1-2), (2-3), (3-4) (4-5).
 

Riassumendo: se viene eliminato un termine intermedio tra i candidati presenti in una cella della sequenza, la modifica riguarderà solo la cella in questione. Se viene eliminato invece il termine minimo (o quello massimo) in una cella della sequenza, allora si avrà una reazione a catena in cui dovremo togliere il termine minimo (o il massimo) in ognuna delle celle successive (o precedenti) a quella in cui è avvenuta la prima cancellazione.

Dopo aver completato l'elenco dei candidati nelle celle che formano le varie sequenze ordinate, procederemo ad inserire i candidati in tutte le altre celle, tenendo conto per esse della sola presenza di cifre già inserite in altre celle della stessa colonna o della stessa riga, che non potranno essere candidate in nessuna delle celle allineate ad esse.

6 - Solitari, doppiette, triplette, ecc.
Una volta che in tutte le celle vuote saranno stati inseriti (a matita) i possibili candidati alla soluzione, iniziamo una sistematica perlustrazione delle celle di ognuna delle righe e di ognuna delle colonne, alla caccia di solitari, doppiette, triplette e così via.
Un solitario è un numero che compare una sola volta nelle celle di una stessa riga o colonna. Esso costituirà la soluzione per la cella che lo contiene. La cifra trovata si scriverà col pennarello, cancellando tutti i precedenti candidati che erano stati inseriti a matita.
Una doppietta è costituita da una coppia di cifre presenti in due sole celle di una stessa riga o di una stessa colonna. Non sappiamo ancora quale delle due mettere in una cella e quale nell'altra; nel frattempo elimineremo in tali due celle tutti gli altri eventuali candidati presenti.
Lo stesso discorso vale per le triplette, quartetti, ecc. presenti in altrettante celle della stessa riga o colonna.

7 – Verso la soluzione
In genere, usando le suddette strategie, che consentono di ridurre i possibili candidati nelle varie celle, si riuscirà a trovare la cifra risolutiva in qualcuna di esse. Ciò farà scomparire la cifra dalle liste di candidati presenti nelle rimanenti celle allineate lungo la stessa riga o colonna, con possibili ripercussioni a catena, come ad esempio nel caso che sia stata eliminata la cifra iniziale o finale in una cella facente parte di una sequenza ordinata (vedi. § 4), oppure sia stata eliminata un delle cifre di una doppietta, nel qual caso avremo la soluzione per entrambe le celle della stessa. Emergeranno così altri possibili solitari o doppiette, ecc. accelerando il percorso verso la soluzione del gioco.

8 – Il metodo dei tentativi ed errori nelle situazioni di stallo
Non sempre le cose filano lisce. Può capitare di trovarsi in una situazione di stallo: abbiamo completato l'elenco dei candidati all'interno di ogni cella, ma non riusciamo a scovare una situazione che ci consenta di prendere decisioni definitive. Nel sudoku, che è costituito da 81 celle, tale situazione è abbastanza frequente. Il caso è molto più raro nel futoshiki, costituito al massimo da 49 celle. Se tuttavia dovesse capitare, potremmo prendere in esame una coppia di celle da assegnare ad una doppietta, oppure una cifra che sia candidata solo due volte in una riga o colonna. Non abbiamo elementi per decidere quale delle due celle assegnare. Decidiamo allora di fare un tentativo, assegnando d'ufficio le due celle a ciascun elemento della coppia o una delle due celle alla cifra singola. Terremo presente la situazione della riga e della colonna prossime alle due celle prese in esame, così come un giocatore di scacchi che esamina tutte le possibili mosse e contromosse prima di muovere un pezzo. Sceglieremo la via che ci sembrerà più produttiva ai fini del proseguimento dei gioco. Non è detto che la via più promettente sia quella buona, ma è sempre meglio così, piuttosto che affidarci solo al caso. Una volta assunta la decisione, si riprende il gioco. Nella maggior parte dei casi si riesce a superare lo stallo e il gioco riprende vigore. L'aver eliminato candidati sistemati, sia pure in via provvisoria, riduce la lista dei candidati nelle altre celle e si scopre che in alcune di esse resta di nuovo un solo candidato. Se la scelta fatta è stata quella giusta, si potrà arrivare a completare l'intero schema. Se invece avremo fatto la scelta sbagliata, finiremo prima o poi per trovarci in una situazione contraddittoria: ad esempio in una certa cella andrebbe messa per forza una certa cifra, ma nel corso del nostro tentativo essa ha già trovato posto in un'altra cella della riga o colonna e non è quindi possibile inserirla una seconda volta. In tal caso dovremo riprendere dal punto in cui eravamo, prima di fare il nostro tentativo. L'aver scelto di lavorare su due sole possibili celle, ci facilita il compito: se prima avevamo sistemato le cifre in un certo ordine nelle due celle, basterà invertire l'ordine, assegnando al contrario le due celle a ciascuna cifra della doppietta o assegnando alla cifra singola l'altra cella disponibile. Questa volta siamo certi di non sbagliare: se ci sono due soli modi per sistemare due celle, sicuramente uno di essi è quello giusto. Non è detto che questa volta arriveremo, senza ulteriori intoppi, fino alla soluzione del gioco. E' possibile trovare situazioni piuttosto complesse, in cui è necessario usare più di una volta il metodo dei tentativi ed errori, prima di sbloccare definitivamente una situazione di stallo. E' una situazione estremamente rara nel gioco del futoshiki, che rimane comunque un gioco di abilità, di intuizione, ma anche di pazienza.

9 – Dalla teoria alla pratica. Un primo esempio non troppo difficile.

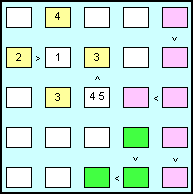
Armiamoci di matita, gomma,  pennarello e ... pazienza, e cominciamo ad esaminare lo schema proposto (ai lettori di questo articolo consigliamo di copiarlo su un foglio a quadretti grandi, eseguendo su di esso le operazioni descritte in seguito). Le celle gialle contengono i dati iniziali, che non possono essere cambiati. Intravediamo subito una cella con la soluzione già pronta. A destra del 2 nella seconda riga  dobbiamo inserire un numero minore di 2: l'unico possibile è il numero 1.  Nella cella sotto al 3 della  seconda riga possiamo anche inserire i due possibili candidati superiori al numero tre: 4 e 5. Passiamo ora ad occuparci delle sequenze ordinate: in verde abbiamo evidenziato una sequenza di tre celle.

Ogni sequenza avrà (5-3+1) = 3 termini: la prima cella (1 2 3), le altre celle, a seguire avranno (2 3 4) e (3 4 5). Osserviamo che nella terza colonna è già presente il 3, pertanto escluderemo tale candidato nella prima cella della serie, che conterrà solo la coppia di candidati(1 2). Nelle celle color lilla sono evidenziate le sequenze di due sole celle. In esse andranno inseriti i candidati (1234) e (2345), escludendo, se occorre, quelli già presenti nella riga o nella colonna.

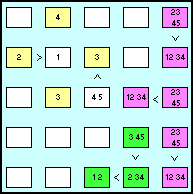
Nella  seconda riga sono già presenti i numeri 1 2 e3. Togliendo tali candidati dalla cella lilla, in essa resta solo il 4. Di conseguenza, nella cella lilla al di sopra andrà il 5. Come abbiamo detto più volte, dopo aver inserito le soluzioni definitive in alcune celle, occorre eliminare tali cifre dai candidati presenti nelle altre celle delle righe e delle colonne corrispondenti ad esse. Nella quinta cella della terza riga dovremo togliere il 4 e il 5, che abbiamo appena inserito, e il 3 che è presente nella riga. Resterà solo il 2 e, di conseguenza, nella cella rosa a sinistra andrà l'1. A questo punto, nella quinta colonna, avendo inserito i numeri 2, 4 e 5. resteranno disponibili solo l'1 e il 3, che andranno nelle ultime due celle lilla in basso ( 3 sopra e 1 sotto). Per finire, l'inserimento dell'1 nella quinta cella dell'ultima riga, farà eliminare l'1 dalla cella verde, in cui resterà solo il 2.

Ecco come si presenta il nostro futoshiki dopo le modifiche. Avendo esaurito il lavoro nelle celle che costituiscono le sequenze ordinate, passiamo a riempire di candidati le celle non ordinate. Una di esse ha già pronta la soluzione: è la cella superstite della seconda riga, in cui scriveremo l'ultima cifra ancora disponibile, il 5. Ciò determinerà quella che abbiamo chiamato reazione a catena nelle due celle verdi in basso, in cui dovremo togliere rispettivamente il 5 e il 4. Resteranno i esse rispettivamente il 4 e il 3. A questo punto, nella quarta colonna resterà da riempire l'unica cella ancora vuota, la prima in alto, in cui non resterà che inserire il 2.

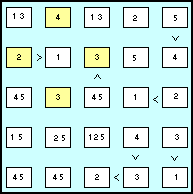
Continuiamo il nostro lavoro con le altre celle ancora prive di candidati, aiutati dagli appunti a matita che avremo scritto nei margini bianchi, con l'indicazione delle cifre che restano ancora da inserire nelle varie righe e colonne.

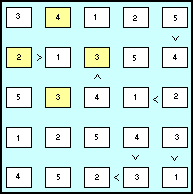
Nella terza cella della prima riga dobbiamo eliminare il 3, già presente nella terza colonna. Resterà l'1 e di conseguenza nella prima cella andrà il 3. Nella terza cella quarta riga ora rimane solo il 5 (avendo appena inserito l'1 ed essendo già presente il 2 nella colonna). Iniziano  a questo punto una serie di inserimenti nelle celle delle varie righe o colonne interessate alle recenti modifiche: 4  e 5 nella terza riga; 1  e 2 nella quarta riga. 4 e 5 nella quinta riga Si completa così il nostro  futoshiki.

10 – Saliamo di livello con un  esempio di rango 6

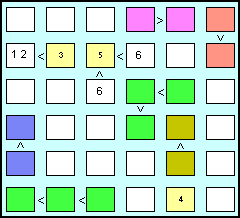
Un paio di celle hanno la soluzione già pronta: sono quelle a destra e sotto la cella con il numero 5, dato che l'unico valore maggiore di 5 è il 6 per entrambe le celle. Possiamo anche indicare i candidati nella cella a sinistra del 3, con i valori (1 2). Dopo questi primi passi che, per la loro semplicità, definirei di ... incoraggiamento, passiamo al consueto esame delle celle che fanno parte delle sequenze ordinate. Ce ne sono un paio di lunghezza tre, evidenziate in verde. Ogni cella avrà una serie di (6-3+1), cioè 4 candidati. La prima cella avrà  la serie (1 2 3 4); le altre celle a seguire avranno (2, 3, 4, 5) e (3 4 5 6). Dalle suddette serie vanno tolti, come abbiamo ripetuto più volte, i candidati già presenti nelle colonne o nelle righe allineate con ciascuna cella della sequenza.

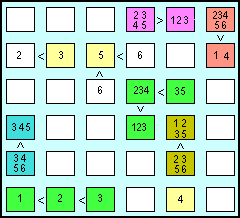
Tra i candidati da eliminare c'è il 6 che abbiamo inserito ai lati del 5 della cella gialla 5. Poiché il 6 è l'elemento più alto della sequenza, si avrà la già nota reazione a catena,  che farà eliminare la cifra più alta nelle altre celle della sequenza. Per le tre celle verdi nell'ultima riga, le suddette cancellazioni, combinate tra loro, faranno pervenire direttamente alla soluzione: la terza cella, che doveva contenere la serie (3 4 5 6), non può contenere il 5 e il 6 presenti nella colonna e neppure il 4 presente nella riga. Resterà solo il 3; è pertanto automatico inserire a ritroso 2 e 1 nelle due celle verdi precedenti: ciò avrà ulteriori ripercussioni nelle altre celle allineate ad esse. Nella prima cella delle seconda riga  resterà il solo valore 2,  che a sua volta farà eliminare il 2 nelle rimanenti celle allineate ad essa.

Le sequenze di lunghezza due, evidenziate con i colori lilla, arancione, azzurro e ocra, avranno al loro interno le due sequenze (1 2 3 4 5 ) e (2 3 4 5 6), sempre al netto di eventuali doppioni già presenti nelle rispettive righe o colonne. La figura a lato evidenzia la situazione dopo l'inserimento dei candidati o delle soluzioni nelle celle ordinate.

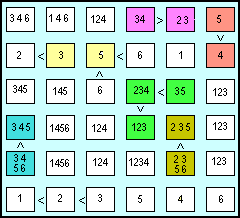
E' ora il momento di passare alle celle non ordinate, che riempiremo con le cifre mancanti nelle righe e colonne relative a ciascuna di esse. Cominciamo dalle righe o colonne con il minor numero di celle vuote. La sesta riga ha due celle libere in cui inserire il 5 e il 6. Non potendo mettere il 6 nella quarta cella, la cui colonna ha già un 6, metteremo in essa il 5, lasciando il 6 all'ultima celle ancora libera. Anche la seconda riga ha due soli numeri mancanti, l'1 e il 4. Non potendo mettere il 4 nella quinta cella (la cui colonna contiene già il 4), non resta che scrivere 1, lasciando al 4 l'ultima cella (arancione). Adesso la cella arancione al di sopra potrà contenere solo il 5 o il 6, ma abbiamo già inserito il 6 nella sesta colonna, perciò non resta che scrivere 5. Completiamo le rimanenti celle bianche, inserendo in esse i candidati  che restano ancora da inserire, nelle rispettive righe e colonne.

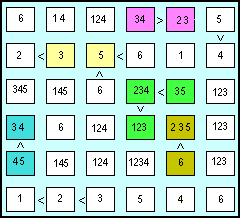
Diamo uno sguardo analitico allo schema, alla caccia di singoletti, doppiette, triplette, ecc. Scopriamo così che la quarta riga ha un solo 6 nella seconda cella. Possiamo escludere allora gli altri candidati e scrivere 6. Questa cifra sarà eliminata in tutte le celle della seconda colonna. Ora anche la prima riga ha il 6 candidato solo nella prima cella. Scriviamo in essa il 6 e cancelliamolo dalla altre celle della prima colonna. A questo punto resta un solo 6 da inserire, quello nella cella ocra in basso.

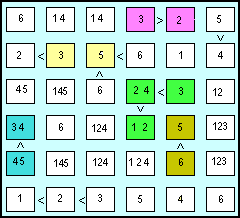
Andando a controllare la cella ocra al di sopra, ci accorgiamo che essa è l'unica della quarta riga a candidare il 5, che risulterà vincente (!)  sugli altri candidati. A seguire nella quinta colonna dovremo anche mettere il 3 nella cella verde e il 2 in quella lilla. Nella cella lilla a sinistra resta allora  l'unico 3 candidato della prima fila. L'inserimento del 3 nell'ultima cella della sequenza ordinata verde, ci obbliga a scrivere il 2 e poi l'1 nella altre due celle verdi. Prima di procedere ad ulteriori passi, è bene dare una "ripulita" alle celle rimanenti, eliminando in esse i numeri che abbiamo appena inserito nei passaggi precedenti.

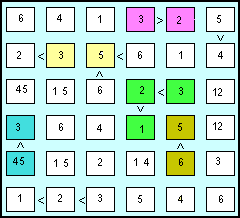
Ecco ora la nuova situazione. Il lavoro di ripulitura ci consente di scoprire la doppietta (4 5) nella  prima colonna. Possiamo così escludere il 4 nella quarta cella, dove resterà il 3, che farà eliminare l'altro 3 nell'ultima cella della stessa riga. Ora la sesta colonna presenta  la  doppietta (1 2), che consentirà di eliminare 1 e 2 dalla quinta cella, dove resterà il 3 . Nella quarta riga  c'è   da inserire il 2 nell'ultima cella. Ciò consentirà di scrivere 4 nella terza cella e, a seguire, un 1 nella prima riga, un 4 nella cella alla sua  sinistra, poi ancora un 2 nella quinta cella della terza colonna.

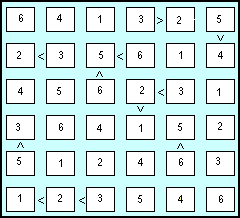
Occorre procedere ad una nuova ripulita eliminando i candidati incompatibili con le cifre appena  inserite. Con il nuovo schema, molto più chiaro dopo il "lavaggio", procediamo ad ulteriori inserimenti. Le prossime mosse ci permetteranno di arrivare alla soluzione: 1 e 2 nella terza e quarta cella della 6^ colonna; 5 e 4  nella seconda e prima cella della 3^ riga; 1, 4, e 5  nella seconda, quarta e prima cella della 5^ riga. Fine!

11 – Saliamo al settimo livello.

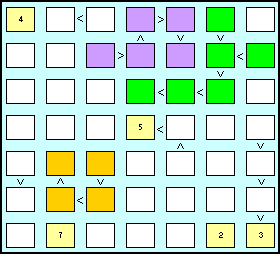
Il futoshiki 7 ´ 7 ha una difficoltà maggiore rispetto ai livelli precedenti, se non altro per il maggior numero di celle. La difficoltà è spesso attenuata dalla presenza di un maggior numero di celle già definite e dai molti segni matematici di ordinamento, alcuni dei quali formano catene piuttosto lunghe. Nell'esempio a lato ci sono quattro celle gialle con il contenuto già definito. Le celle color lilla evidenziano una sequenze ordinata di 5 caselle. Quelle verdi indicano due sequenze, sempre di 5 caselle, con i primi quattro elementi in comune e una biforcazione dopo la quarta cella che conduce a due diversi punti di arrivo. Ogni cella della sequenza avrà (7-5+1) cioè 3 candidati in ciascuna cella. La prima cella di ciascuna delle suddette  sequenze avrà i numeri (1 2 3); a seguire le celle successive, conterranno come candidati le serie (2 3 4), (3 4 5), (4 5 6) e (5 6 7).

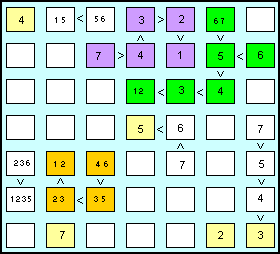
Tutte le serie indicate sono "al lordo" di eventuali numeri già presenti in alcune righe o colonne, che andranno quindi tolti nelle celle allineate ad esse. Nelle celle lilla, in particolare, la presenza di un 4 nella riga e di un 5 nella colonna, farà ridurre al solo 3 il candidato nella quarta cella della prima riga.  A ritroso, avremo 2  e 1 nelle due celle lilla che lo precedono nella sequenza. Nelle due sequenze verdi, quella che termina nella sesta colonna non può avere il 7 (termine massimo) di conseguenza avrà il  la copia 5-6; a ritroso, le celle verdi saranno formate da (4 5), (3 4), (2 3) e (1 2) ma nella  cella (2 3) non potendo esserci il 2, resterà il 3 e, a cascata, nelle successive celle verdi metteremo il  4, il 5 e il 6. Resterà invece la coppia (6 7) nella cella verde della prima riga. A questo punto, per la presenza del 5 e del 6 verdi nella seconda riga le rimanenti celle lilla della stessa riga avranno il 4 e il 7.

La sequenza arancione da quattro caselle avrà nell'ordine le serie (1 2 3 4), (2 3 4 5), (3 4 5 6) e (4 5 6 7). Osserviamo però che il 7 è già presente nella quinta riga  (dove finisce la sequenza) e quindi, per la nota reazione a catena, la sequenza nelle celle arancione sarà così ridotta: (1 2 3 ), (2 3 4), (3 4 5) e  (4 5 6), che dovremo ulteriormente ridurre, osservando i numero allineati con ciascuna di esse. Abbiamo poi una sequenza da tre caselle, che ha come punto di partenza la cella gialla con il 5 e come valori obbligati, il 6 e il 7 nelle altre due celle. La sequenza di quattro celle con partenza dal numero 3 in basso a destra, dovrebbe avere le serie (4 5), (5 6) e (6 7) nelle tre celle al di sopra. L'ultima di esse però non può contenere il 6, inserito in precedenza nella quarta riga, e pertanto avrà il solo valore definitivo 7.  La presenza del 6 verde in alto, farà ridurre anche le altre due celle della sequenza ai soli valori 5 e 4. Restano ora le due sequenze di due caselle nella prima riga e nella prima colonna. In esse dovrebbero andare le due serie (1 2 3 4 5 6) e (2 3 4 5 6 7 ) ma la presenza di altri numeri nelle loro righe e colonne, farà ridurre ulteriormente i candidati nella sequenza della prima colonna ai soli valori (2 3 6) e (1 2 3 5) e nella prima riga  alle due serie (1 5) e (5 6). Passiamo ora alle celle non ordinate, compilando per ciascuna di esse le liste dei candidati. In questo lavoro ci saranno di aiuto gli appunti  scritti nei margini esterni allo schema, in cui avremo elencato i numeri mancanti nelle varie righe e colonne.

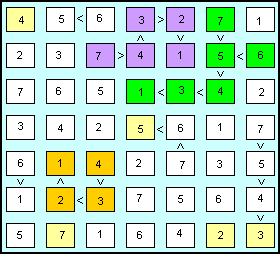
Cominciamo dalle righe e colonne con il minor numero di celle vuote. Nella settima colonna mancano le cifre 1 e 2; non possiamo usare il 2 nella cella in alto, dove andrà l'1; al 2 resterà la terza cella. L'inserimento dell'1 nella prima riga farà risolvere  anche le altre tre celle della riga stessa: il 5 e il 6 nella seconda e terza cella e il 7 nella cella verde. Anche la cella verde della terza riga potrà escludere il 2 e resterà l'1. Nella quinta colonna mancano i numeri 4 e 5 nelle due celle in basso. Non possiamo usare il 4 nella sesta riga, quindi metteremo il 5 sopra e il 4 sotto. I recenti inserimenti determinano la soluzione della sequenza arancione: l'ultima cella con può più contenere il 6 (presente nella colonna) e resterà il 4; a ritroso completiamo la sequenza con i rimanenti numeri 3, 2, e 1. Nella seconda riga mancano il  2 e il  3 nelle prime due celle.

Non potendo usare il 2  nella seconda cella, scriveremo nell'ordine 2 e 3. Nella sesta riga la prima cella non può più contenere il 2, 3 e 5 e quindi resterà l'1. Completiamo con il 6 e 7 anche le altre due celle, mettendo il 6 nella sesta cella (in cui non può essere usato il 7) e il 7 nella quarta.
Seguono ora una serie di inserimenti, che ci conducono rapidamente alla soluzione:
1 e 3 nella sesta colonna;
6 e 2 nella quinta riga;
6, 5 e 1 nella settima riga
5 e 2 nella terza colonna
4 e 6 nella seconda colonna
3 e 7 nella prima colonna.
Si conclude qui la nostra breve guida al futoshiki, meno noto del sudoku, ma altrettanto interessante come passatempo per riempire qualche ora vuota della giornata.

Vittorio De Petris