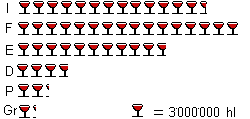18 - Rappresentazione dei dati statistici.   All'inizio di questa breve escursione nel mondo della statistica abbiamo detto che una della sue caratteristiche è quella di trattare grandi masse di dati, ricavandone un ristretto numero di informazioni che, in maniera estremamente sintetica, fossero in grado descrivere il fenomeno osservato. Cosa c'è di più sintetico di un grafico? Le immagini vengono afferrate rapidamente e un occhio esperto è in grado di ricavarne un bel numero di informazioni. Ecco alcuni dei tipici grafici usati in statistica:   Grafico cartesiano.   Serve a mettere in relazione due variabili a carattere continuo, a partire da un insieme discreto di valori osservati. Per ciascuna coppia di valori corrispondenti delle due variabili, si determina un punto sul piano; collegando fra loro i punti ottenuti, si ottiene una linea spezzata che esprime, con una certa approssimazione l'andamento delle due variabili nel continuo. È quanto fanno le infermiere all'ospedale, quando registrano su un grafico la temperatura presa ad intervalli di tempo durante il giorno.   Istogramma e ortogramma.  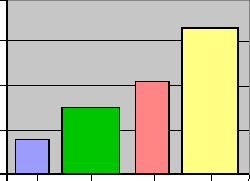 Costituiscono rappresentazioni classiche. Su di un piano si riportano rettangoli di varia altezza, proporzionale all'intensità del fenomeno descritto; gli ortogrammi, detti anche diagrammi a barre, sono costituiti da rettangoli di uguale base; pertanto la misura da essi rappresentata è espressa semplicemente dall'altezza; negli istogrammi si può avere una base diversa per ogni rettangolo, quando vengono raggruppate fra loro classi contigue (ad esempio le 3 classi di età della scuola materna, le 5 classi della scuola elementare, le 3 classi della media ecc). Per motivi di impaginazione i diagrammi a barre possono essere disposti anche orizzontalmente. In alcuni casi i rettangoli sono contigui; in altri vi è una spaziatura fra un rettangolo e l'altro; sarebbe bene che i primi fossero usati nei fenomeni a carattere continuo (esempio la pioggia nei vari mesi dell'anno); non ha molto senso usare rettangoli contigui per rappresentare la popolazione dei vari stati; in tal caso gli ortogrammi esprimono la sola dimensione verticale. Non vi è infatti un asse delle ascisse (i1 nome di uno stato non è una variabile in senso matematico).   Diagramma a coordinate polari. 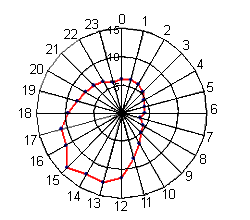  Si usa per rappresentare fenomeni ciclici, nei quali, al termine di un ciclo (giornaliero, settimanale, stagionale, ecc.) il fenomeno si ripresenta di nuovo. Il diagramma si ottiene dividendo il ciclo in un certo numero di parti uguali, ciascuna delle quali è rappresentata da un raggio dei corrispondenti settori in cui il cerchio viene suddiviso. Ad esempio, un ciclo di 24 ore sarà rappresentato da un cerchio diviso i 24 settori uguali. Su ciascun raggio si riporta l'estremo di un segmento di lunghezza proporzionale alla misura da rappresentare (il valore massimo non deve superare la lunghezza di un raggio; collegando fra loro gli estremi di tali segmenti, si otterrà un grafico continuo, il cui significato sta nella maggiore o minore distanza dal centro. Sovrapponendo più grafici, si potranno evidenziare le differenze di tendenza del fenomeno analizzato. Il diagramma a lato è un esempio del variare della temperatura nelle 24 ore presumibilmente in una giornata invernale.   Aerogramma circolare. 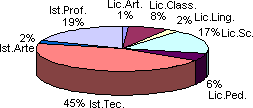  È il più noto dei diagrammi usati in statistica, chiamato anche diagramma a torta. Corrisponde ad un partizione di un insieme, in cui ogni parte è rappresentata proporzionalmente da una fetta della torta. Vengono adoperati quando le parti da rappresentare non sono molto numerose e costituiscono una partizione di un dominio chiuso. Se le parti fossero troppo numerose si avrebbero diagrammi troppo frazionati e di difficile lettura. In tala caso sarebbe consigliabile formare dei raggruppamenti.   Ideogramma. 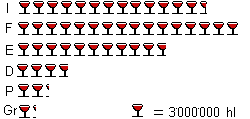  I valori sono rappresentati da figurine, a ciascuna delle quali corrisponde un certo numero di unità; ad esempio un bicchiere di vino rappresenta 3.000.000 hl; più figurine, messe una a fianco all'altra a distanze regolari daranno una rappresentazione (molto grossolana) dell'intensità del dato complessivo rappresentato. Gli ideogrammi sono sostanzialmente analoghi ai diagrammi a barre, resi pił accattivanti dalle immagini, che suggeriscono anche la natura del fenomeno descritto. In alcuni casi si fanno figure più o meno grandi per indicare le quantità da rappresentare, ma tale rappresentazione può trarre in inganno, poiché il rapporto di similitudine per i volumi è uguale al cubo di quello tra le lunghezze. Un bicchiere alto e largo il doppio conterrà quindi una quantità di vino otto volte maggiore. D'altro canto, rispettando le proporzioni, in base al volume, il grafico potrebbe trarre in inganno, non essendo facile stimare ad  occhio volumi differenti.   Cartogramma. 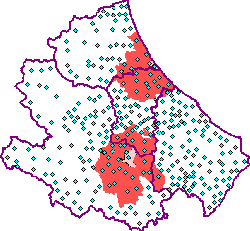  È di difficile realizzazione. Occorre conoscere il modo in cui i dati sono distribuiti all'interno di un certo  territorio. Una cartina geografica della regione interessata viene suddivisa in parti (es. province), ciascuna delle quali viene riempita con un colore convenzionale secondo una scala colorimetrica riportata a fianco. In altro criterio è quello di riportare puntini più o meno addensati nelle zone in cui il fenomeno appare più o meno diffuso. Sia la scala colorimetrica, sia i singoli puntini recano a lato il valore di riferimento. Ovviamente, per la scala colorimetrica, non potendo usare infiniti colori, si assegnerà a ciascun colore un determinato intervallo di valori di riferimento, ad esempio da 10.000 a 20.000. La mappa a lato rappresenta gli ambiti locali di 20 km distribuiti nel territorio abruzzese. Test di verifica con 30 domande