11 - Correlazione statistica.   Ancora foglie! Ne basteranno una quarantina. La scelta questa volta non sarà casuale poiché ne occorreranno di varie grandezze assortite, piccole, medie e grandi. A prima vista è facile rendersi conto che le più lunghe sono anche le più larghe; tuttavia vogliamo esaminare un po' più da vicino il fenomeno, per scoprire che tipo di relazione vi sia tra le due suddette misure. Ovviamente il metodo che seguiremo si presta ad essere adoperato in una grande varietà di casi, ogni volta che vorremo indagare su eventuali correlazioni tra due fenomeni diversi (es. costo del biglietto e numero di spettatori) o tra due o più caratteri rilevati su ciascun individuo di una certa popolazione (ad esempio altezza di un individuo e lunghezza della sua spanna), messi in corrispondenza tra loro. Nella tabella a lato abbiamo riportato le misure di una quarantina di foglie. 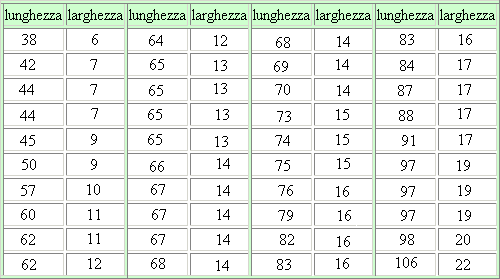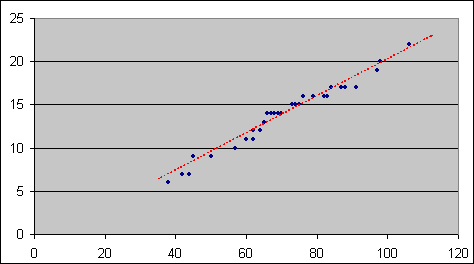Riportiamo i valori ottenuti sul piano cartesiano: ad ogni coppia ordinata (lunghezza, larghezza) corrisponde un punto. Una volta segnati i 40 punti corrispondenti a ciascuna delle coppie di misure di ogni foglia, osserviamo immediatamente che essi sono disposti sul piano cartesiano in modo piuttosto regolare, abbastanza vicini ad una retta ideale che passa attraverso di essi. Se i punti si trovassero esattamente lungo una retta, diremmo che esiste una proporzionalità diretta tra le due grandezze considerate. Nel nostro caso, invece parleremo di correlazione positiva o diretta tra i valori delle lunghezze e quelli della larghezze delle nostre foglie. Al crescere dei valori della prima grandezza tendono a crescere anche i valori della seconda, anche se il rapporto tra le due grandezze non è proprio costante: La correlazione è messa in evidenza dall'andamento inclinato verso l'alto della "nuvola di punti da noi realizzata.