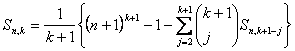Sunto: Partendo dalla curiosità sollecitata da un quesito assegnato agli esami di Stato, si ricava una formula ricorsiva per il calcolo della somma delle potenze di grado k dei primi n numeri naturali.

1 - Premessa

Considerati i primi n numeri naturali a partire da 1:
1, 2, 3, 4, ...., n
moltiplicarli combinandoli in tutti i modi possibili. La somma dei prodotti ottenuti risulta uguale a:

A)

B)

C)

D)

Una sola risposta è corretta: individuarla e fornire una spiegazione esauriente della scelta operata.

La risposta corretta è la A) è può essere giustificata come segue.
Per ottenere tutti i possibili prodotti, moltiplichiamo i primi n numeri naturali per 1, 2, 3, ..., (n-1), n, ottenendo il seguente quadro:

1·1,   2·1,   3·1,   ...,  (n-1)·1,   n·1
1·2,   2·2,   3·2,   ..., (n-1)·2,   n·2
1·3,   2·3,   3·3,   ..., (n-1)·3,   n·3
..............................
1·n,   2·n,   3·n,   ...,  (n-1)·n,   n·n

Sommando i prodotti per colonna e indicando con S_tot la somma richiesta e con S_n la somma dei primi n numeri naturali, si ottiene:

(1.1)

Da cui, mettendo in evidenza S_n, si ottiene:

(1.2)

La lettura e la risoluzione del quesito sollecitano due curiosità: quella di ritrovare una formula generale per calcolare le somme delle potenze dei primi n numeri naturali con dato esponente e poi quella di vedere se anche le espressioni delle altre risposte proposte hanno una qualche relazione con esse.

2  - Somma delle potenze dei primi numeri naturali allo stesso esponente naturale

Fissati i numeri naturali n e k, poniamo:

(2.1)

Per k=0 si ottiene S_n,0 = n; per k=1 si ottiene facilmente

(2.2)

Allo scopo di trovare una formula che ci consenta di calcolare S_n,k per ogni valore di n e di k, consideriamo l'identità

Assegnando a p, nella precedente identità, i valori naturali da 1 ad n, si ottengono le n uguaglianze:

...................................
 

Sommando membro a membro le n uguaglianze, si ottiene:

(2.3)

Esplicitando nella (2.3) il secondo membro e ricavando S_n,k  , si ottiene la formula che, tenendo conto che risulta S_n,0  = n, ci consente di calcolare la somma delle potenze di grado k dei primi n numeri naturali per ogni valore di k e di n.

(2.4)

Dalla (2.4), tenuto conto della (2.2), possono essere ottenute facilmente le somme dei quadrati, dei cubi e delle quarte potenze.

Tenuto conto della (2.4), possiamo osservare che S_n,k  è sempre un polinomio di grado k + 1 nella variabile n.
E' poi possibile vedere che due delle altre tre risposte proposte per il quesito assegnato all'esame di Stato sono effettivamente in relazione con somme S_n,k.