Goldbach: Ogni numero pari superiore a 2 è la somma di due numeri primi.

Da duecento anni buoni esiste questo enigma sui numeri primi, i quali tuttavia esistono da oltre duemila anni. Fin dall'antichità dunque il problema sollevato da Goldbach si trova accanto a questi numeri e ora, insieme, si disputano il favore dei matematici. Dopo che Euclide ebbe a dimostrare che la quantità dei numeri primi è infinita, la matematica tradizionale ne ha definito il ruolo, enunciando che essi formano la base moltiplicativa del sistema dei numeri interi. In altri termini, ogni numero intero maggiore di 1 è o primo o il prodotto di un unico insieme di numeri primi. Su questa base, i numeri composti si esprimono come prodotti di due o più fattori primi e l'aritmetica, nell'abbracciare l'insieme delle due categorie, definisce i numeri naturali.

Un metodo costruttivo per separare i numeri primi dai numeri composti presenti in una successione finita di numeri naturali viene attribuito al filosofo greco Eratostene. Tramandato dalla matematica, nel tempo, con il nome di Crivello di Eratostene, il sistema può essere espresso nel modo seguente: ogni numero composto a, di una successione di numeri naturali non superiori a un dato numero n, cade da un setaccio virtuale in corrispondenza del più piccolo dei suoi divisori primi ^*.

(*) Se p è il più piccolo divisore primo di a, con a = p·r, allora r ³p. Segue che a = p·r ³ p·p = p2, da cui p £ Ö a.

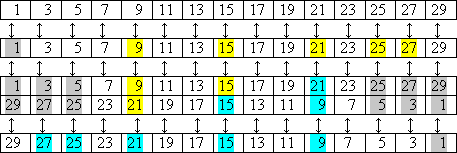
Il modo migliore per chiarire come opera questo principio consiste nella sua applicazione pratica. Per prima cosa si redige la successione dei naturali da setacciare, ad esempio, quella fino al 13:

Poi, si cancellano i numeri che, a partire dal 2, si incontrano ogni due passi (ossia i multipli del 2):

Successivamente si cancellano i numeri che, a partire dal 3, si incontrano ogni tre passi (cioè i multipli del 3), contando anche quelli che eventualmente fossero stati già cancellati:

In questo caso, il procedimento si conclude con i multipli del 3 perché questo numero è il massimo intero il cui quadrato non supera l'ultimo numero della successione.

Dovrebbe esser chiaro che i numeri che non sono stati evidenziati sono quelli che restano nel setaccio, e tali sono i numeri primi della successione dei naturali fino al 13:

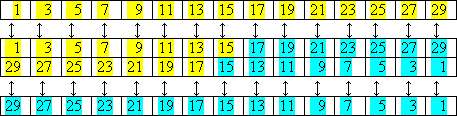
Ripetendo la procedura sulla stessa successione scritta alla rovescia, si ottengono gli stessi risultati del processo originale, ovviamente a termini invertiti:

L'accoppiamento dei risultati delle due setacciature mostra che, se si lasciano i termini ai loro posti, il numero pari 14 si ottiene in due modi, entrambi come somma di due numeri primi:

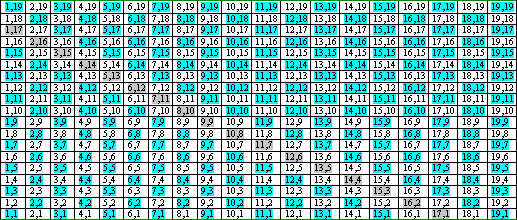
Quanto è stato ottenuto per il numero 14 può essere replicato all'infinito per ogni numero pari, semplicemente contrapponendo fra loro tutte le successioni dispari dei naturali.

Tuttavia, da quanto si è visto ora per il numero 14 non discende alcuna certezza che le coppie dei numeri primi si riformeranno sempre. Questi numeri hanno un andamento indescrivibile e per di più nelle successioni maggiori, formate da quantità incalcolabili di miliardi di naturali, divengono sempre più rari; per quale miracolo mai due di essi dovrebbero sempre appaiarsi?

Storicamente, molti enunciati sui numeri primi sono stati dimostrati con metodi elementari. Qui, il tentativo di chiarire le ragioni di Goldbach si fonda sul fatto che l'esistenza dei numeri composti è connessa all'accostamento dei numeri primi e che essa costituisce un'esigenza della teoria dei numeri perché altrimenti il loro ordinamento sarebbe incompleto.

Per chiarire come opera questa esigenza, si deve iniziare dal Sistema Cartesiano. Esso può essere visto come l'insieme dei punti del piano i cui valori, x e y, formano un reticolo di coppie ordinate in formazione quadrata. Una porzione finita, in cui le coordinate variano da 1 a 19, è rappresentata nella figura seguente:

Le coppie dei numeri che formano le diagonali che vanno dall'alto a sinistra a destra in basso del reticolo sono formate da due successioni uguali di naturali che si accrescono in direzioni opposte e, se x è un elemento, il suo coniugato y è tale che Δ x + Δ y = costante. . Le somme di queste diagonali si succedono seguendo l'ordine dei naturali: 2,3,4,...

La diagonale evidenziata in grigio sulla figura precedente è tale che Δ x + Δ y = 18:

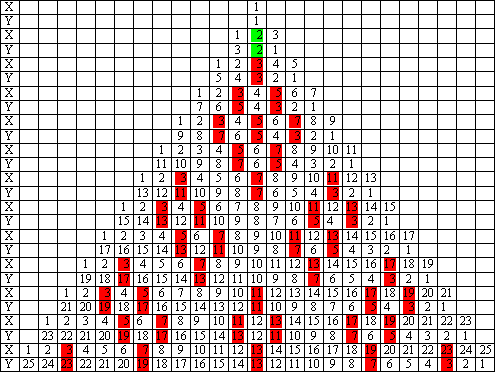
Poiché l'interesse di questo lavoro è volto esclusivamente alle diagonali che hanno per somma un numero pari, tutte le altre, le cui somme producono i numeri dispari, possono venire cassate dal reticolo.

Una porzione finita del reticolo residuo ove le coordinate variano da 1 a 13 è mostrata nella figura seguente (il reticolo è stato ruotato di 135° in senso orario; le coppie composte unicamente da numeri primi dispari sono evidenziate in rosso):

Questa particolare rappresentazione del reticolo suggerisce la sostituzione del termine diagonale con quello più consono di serie orizzontale di coppie, che d'ora in poi si utilizzerà nella forma abbreviata di serie.

Le due successioni di numeri che formano le coppie della colonna centrale del reticolo seguono l'ordinamento dei numeri naturali e, qualunque sia l'elemento di riferimento n₁, n₂, n₃,...di N, la relativa coppia si può caratterizzare come l'elemento t_p pari:

Se a ciò si aggiunge che tutte le serie hanno per somma un numero pari, si deduce facilmente che, per risolvere il problema sollevato da Goldbach, basta spiegare perché non è possibile che fra le coppie che le formano possa mancarne una composta di soli primi.

La figura che segue mostra come ciascuna serie sia costituita degli stessi numeri che formano le coppie della colonna centrale lungo un segmento di pari lunghezza, a partire dalla coppia (1,1):

Nelle due strisce seguenti, si possono osservare in dettaglio il segmento della colonna centrale del reticolo compreso fra le coppie (1,1) e (13,13) e la sua corrispondente serie orizzontale (per maggiore evidenza le due figure sono state poste in parallelo, anziché a croce fra loro):

In fisica, l'affermazione di una costanza nella natura è definita legge di conservazione. Ad esempio, la seconda delle tre leggi relative al moto dei pianeti di Keplero, la cosiddetta legge delle aree, è equivalente ad una legge di conservazione del momento angolare. Secondo questa legge, una corda tesa fra la Terra e il Sole descrive nello spazio un'area costante nell'unità di tempo. Perché questo possa succedere, la Terra deve accelerare o rallentare la sua corsa in relazione alla sua minore o maggiore distanza dal Sole.

Nelle serie che formano il reticolo, non è difficile riconoscere lo stesso modello mentale descritto da Keplero: se x è un elemento di coppia, il suo coniugato y deve essere tale che Δ x + Δ y = costante.

Osservando le simmetrie che fanno da fili conduttori alla collocazione dei numeri sul reticolo, si può notare che le successioni dei naturali che dai due lati dello zero evolvono verso l'infinito sulle serie di coppie orizzontali si corrono incontro. Il valore di queste simmetrie consiste nel fatto che esse impongono delle restrizioni limitanti la libertà dei fattori che formano le coppie. In particolare, l'invarianza speculare impone che il numero dei numeri che si accrescono a destra sia uguale a quello dei numeri che vanno a sinistra, cioè che la distribuzione dei naturali risulti esattamente simmetrica, perché solo in tal caso le successioni sovrapposte sono in accordo fra loro. In questo modo, ogni volta che un fattore di coppia si modifica, il suo coniugato subisce una variazione uguale e contraria, tale da compensarlo esattamente. Ne segue che ogni serie che compone il reticolo, {0, 1, 2, ..., t -1}, con l'operazione di coppia Δ x + Δ y = costante riproduce un gruppo dell'operazione addizione modulo t è dettato dall'invarianza speculare:

Restando sulle conseguenze pratiche che derivano dalle simmetrie ordinatorie del reticolo, un'altra implicazione che occorre notare discende direttamente dal principio di parità. Questa invarianza è importante ed è collegata alle leggi che regolano le operazioni algebriche, ma poiché l'esperienza ordinaria costringe a supporla essa sembra a prima vista banale, o di per sé evidente; qui invece è opportuno esplicitare che, se non fossero entrambi dispari o entrambi pari, i due componenti le coppie non potrebbero mai sommarsi per formare un numero pari:

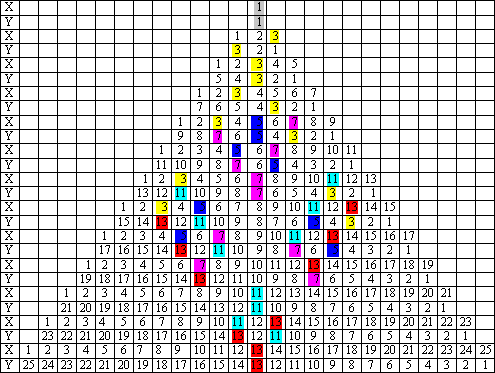
Il termine parità fu usato per la prima volta dai matematici per operare una distinzione fra i numeri pari e dispari: se due interi sono entrambi pari o entrambi dispari si dice che hanno la stessa parità. L'applicazione di questo principio alle serie, oltre a confinare la soluzione del problema sollevato da Goldbach ai soli numeri dispari, rende conto, unitamente al precedente e a una terza simmetria che vede le coppie ordinate scambiarsi le x con le y, di un'altra situazione. Si può immaginare una serie composta da un numero incalcolabile, anzi infinito, di naturali, ma dato che la configurazione è simmetrica rispetto alla coppia centrale consente di prevedere che anche i multipli dei suoi fattori subiranno la medesima simmetria. Per una illustrazione di questo principio, si può assumere la serie Δ x + Δ y = 30 = (2)x3x5 ed eseguirvi la setacciatura di Eratostene. Prendendo in considerazione solo i termini dispari (si osservi la figura sottostante), si inizia dal 3 e, di tre passi in tre passi, si evidenziano in giallo i numeri che si incontrano; si passa poi al 5 e, di cinque passi in cinque passi, si segnano in azzurro i multipli del 5. Poi, si ripetono le stesse operazione sulla successione opposta. I segni lasciati dai colori mostrano che i valori del 3 e del 5, dopo essersi portati entrambi sulla coppia di centro, tornano indietro fino a riportarsi su se stessi:

L'artificio di evidenziare i numeri con i colori è molto di più di un semplice trucco artistico. Esso permette di vedere chiaramente che le coppie colorate hanno un fattore in comune.

Il punto chiave consiste nella stretta relazione che si costituisce fra il meccanismo di formazione di queste particolari coppie e la funzione fondamentale delle leggi di conservazione. Prima di cercare di chiarirne le connessioni, ci si deve porre l'interrogativo retorico: che cosa sono le coppie ordinate se non dei numeri composti ottenuti in modo sistematico?

Restando sull'esempio precedente, si può illustrare l'idea generale prefigurandone la situazione attraverso il solito gioco di colori, riassuntivo delle simmetrie menzionate:

La nuova colorazione fa recuperare all'ambito degli oggetti algebrici ciò che era chiaro solo nella simmetria. Ciascuna delle due successioni (ad esempio quella evidenziata in giallo) è costituita dai naturali fino al 29. In questo caso, il massimo intero il cui quadrato non supera l'ultimo numero è 5, e perciò i numeri composti sono multipli del 3 e del 5 (evidenziati in verde). Questi numeri, nel combinarsi in coppie, divengono multipli dei multipli ^* del 3 e del 5:

(*)Attenzione: multipli dei multipli; il fatto che siano i prodotti dei numeri composti che cadono dal setaccio ha un'importanza decisiva.

I colori rivelano subito la contrazione che si stabilisce a carico del numero dei numeri composti nel passare da composti della successione a composti della serie. A fronte di cinque multipli del 3 e 5 presenti sulla successione, i multipli dei multipli del 3 e 5 presenti sulla serie sono solo quattro.

Si può capire adesso perché nella formazione delle coppie il ruolo ricoperto da quelle che hanno un fattore in comune è importante. Se un numero composto si combina con un primo, nel computo totale si annullano reciprocamente (si vedano i numeri evidenziati in grigio sulla figura seguente), ma se un numero composto si combina con un altro numero composto (numeri evidenziati in giallo e azzurro), allora un numero primo deve necessariamente combinarsi con un altro primo perché solo così può formare una coppia.

L'esempio sembra legato ad un inganno, ma questo non è un inganno menzognero: è vero che per formare le coppie i numeri si dimezzano, ma poiché le successioni sono due, l'insieme si conserva. La corrispondenza tra i naturali, primi e composti, e composti dei naturali n ↔ 2n è biunivoca:

Vale la pena di ripercorrere le tappe della discussione precedente. I naturali della successione sono tanti quante tutte le coppie. Così, quando i numeri composti, combinandosi tra sé, si contraggono, i numeri primi si riuniscono per mantenere costante il numero delle coppie. In effetti, ogni serie, la cui somma sia data da due numeri composti uguali, forma sempre delle coppie con un fattore comune, e perciò l'ipotesi di Goldbach può venire dedotta come semplice conseguenza che la descrizione della comparsa di una coppia di primi è equivalente alla descrizione della scomparsa di un numero composto.

I fisici amano ripetere che ogni fatto della natura trova la sua origine in una legge di conservazione. Solitamente si pensa alla simmetria in termini di spazio (simmetria: com-misurazione), ma in termini speculativi simmetria significa che, mentre una cosa varia in qualche modo particolare, qualche altra cosa si conserva, sia essa una quantità reale, un principio matematico o tutti e due.

La precedente descrizione geometrica della situazione può venire sostituita da una descrizione algebrica. A tal fine è necessario riferirsi all'idea di operazione binaria. Tale è la relazione che assegna ad ogni coppia ordinata un elemento univocamente determinato.

I fattori delle operazioni binarie, generalmente, sono palesi, invece le espressioni che descrivono le serie contengono dei valori che di per se stessi non sono osservabili: Δ x + Δ y = costante. Inoltre, la somma compiuta con una coppia produce lo stesso risultato di tutte le altre e tale uniformità implica l'impossibilità di accertare la composizione assoluta di ciascuna. Nella serie Δ x + Δ y = 30 presa ad esempio, i risultati determinano la probabilità, si dica così, che i fattori componenti le coppie siano 3,5, ma in realtà è una sola coppia che li contiene effettivamente tutti e due.

Ma c'è di più, la stessa operazione di somma può essere messa in discussione, dato che nessun aspetto della composizione di un numero isolato dipende dall'operazione che lo ha prodotto:

Nelle operazioni binarie, coppie ordinate e risultati delle operazioni appaiono, non solo intimamente collegate, ma di fatto la stessa cosa o, più esattamente, aspetti differenti della stessa cosa. E' questo un principio assoluto secondo il quale, in un sistema isolato, quali che siano le sue trasformazioni interne, la composizione resta costante.

Qui interviene l'idea di simmetria: qualsiasi mutamento che si voglia indurre nelle quantità non osservabili (per esempio, passando dalla somma al prodotto, ovvero da una coppia all'altra) senza produrre mutamenti nelle quantità palesi (quali sono i primi componenti le somme e quelli in corrispondenza dei quali i numeri composti cadono dal setaccio) deve lasciare invariato il principio secondo cui se due numeri hanno un fattore comune, quel fattore divide somma e prodotto.

Sebbene questa simmetria si basi, appunto, su di un principio assoluto, la sua applicazione richiede almeno un confronto chiarificatore. La fisica a volte utilizza delle quantità che non sono di per se stesse osservabili. La funzione d'onda per esempio è una di queste. Essa determina la probabilità che l'elettrone si trovi in un luogo particolare dell'atomo di idrogeno, ma non è essa stessa tale probabilità né qualche altra quantità misurabile. Analogamente, nelle serie, i valori x, y componenti le coppie esprimono misure, e precisamente misure rispetto alla loro somma presa come metro di segmenti non maggiori di essa, sono perciò numeri indefiniti compresi fra 0 e 1. Quindi, è logico aspettarsi che la somma di due numeri il cui prodotto è uno sia minima quando sono uguali. Per rendersene conto, si consideri la seguente congettura: fra tutti i rettangoli di area uno, il quadrato ha il perimetro minimo. E' chiaro che un rettangolo lungo e sottile di area uno ha un perimetro molto più grande di uno tozzo avente la stessa area, ed è logico pensare che il quadrato abbia il perimetro minimo poiché è il rettangolo più tozzo. In realtà, si dimostra che, se x > 0, allora x + 1/x ≥ 2.

Ora, quanto c'è da dire su questa simmetria si può accentrare in un esempio: siano due operatori, ciascuno con una operazione di riferimento (somma o prodotto); essi ottengono risultati diversi, ma concordano sull'intero sistema operativo che se i componenti di coppia hanno un fattore comune, quel fattore divide somma e prodotto.

Nella serie Δ x + Δ y = 30, l'insieme dei primi 3 e 5 che formano la somma coincide con l'insieme dei primi in corrispondenza dei quali i numeri composti cadono dal setaccio i quali, a loro volta, formano i multipli dei multipli del 3 e del 5, ossia i prodotti.

Ne segue che, se si adotta come principio di invarianza la divisibilità dei risultati delle operazioni, si può concludere che le coppie che non hanno né il 3 né il 5 come fattore comune, ovvero i risultati dei prodotti che non sono divisibili né per 3 né per 5 non possono essere altro che coppie di primi.

Ciò che la matematica mostra è che, caduti i multipli dei multipli del 3 (colorati in giallo)e del 5 (colorati in azzurro), i restanti numeri primi che compongono la successione, 7,11,13,17,19,23,29 (sono i numeri che restano nel setaccio), per formare delle coppie, devono combinarsi fra loro: (7,23), (11,19), (13,17), (19,11):

Essenzialmente, la questione che solleva la congettura di Goldbach è la seguente: come si può sapere che la presenza delle coppie dei primi sia costante su tutte le serie?

Uno scettico potrebbe obiettare che con gli esempi scelti ad arbitrio, in cui si sa già a priori che le coppie di primi sono presenti nella serie, non c'è da meravigliarsi che poi, a posteriori, si possa fornire una spiegazione della loro presenza.

Ma come si può essere certi che non esista una serie che ne sia priva?

A questa obiezione si possono dare due risposte eccellenti. In primo luogo, occorre considerare che la composizione della coppia centrale di tutte le serie è formata da due numeri dell'ordinamento dei naturali, uguali fra loro, e quindi il risultato della loro somma sarà sempre composto o di due primi (si consideri ad esempio la serie Δ x + Δ y = 14 = 7+7) o di due insiemi uguali di numeri primi. Nel primo caso, la soluzione è già lì. Nel secondo, è importante rendersi conto che il numero dei numeri composti è sempre inferiore al numero dei naturali di ciascuna successione e nel passaggio da semplici numeri composti presenti nelle successioni ai loro composti di coppia questo numero subisce una o più contrazioni dovute alla legge di conservazione dei fattori comuni. Ora, dato che il numero delle coppie è uguale al numero dei naturali che le formano, si può concludere che fra le coppie che formano le serie ce ne saranno sempre alcune formate da soli primi.

Si consideri la serie Δ x + Δ y = 50 = (2)x5x5 → 5. In questo caso, i numeri composti che cadono dal setaccio sono i multipli del 3,5,7; fra questi primi, solo il 5 può dividere somme e prodotti. Ciò comporta che solo questo numero può formare dei multipli con i suoi multipli. Segue che, se i primi residuali (tra cui 3 e 7), non possono formare dei multipli con i loro multipli, per formare delle coppie, devono necessariamente combinarsi con altri primi: (3,47),(7,43),(13,37) e (19,31):

L'altra risposta, fondata su una dimostrazione di esistenza, fornisce la prova conclusiva. Se si mette in relazione la presenza delle coppie di primi sulle serie con la successione dei naturali, per contro, si deve dedurre che l'eventuale mancanza ne violerebbe l'ordinamento, il che è assurdo.

Nella serie Δ x + Δ y = 14, quando dalle somme si passa ai prodotti, anziché assegnare un elemento univocamente determinato da tutte le coppie, Δx + Δ y = t₁₄ → (1 + 13 = 14 ≡ 0), la corrispondenza assegna ad ogni coppia ordinata uno degli interi composti della successione dei naturali fino al 49. In pratica, uno dei fattori che formano le coppie della serie Δ x + Δ y = t₅₀ → (1 + 49 = 50 ≡ 0):

(*) Invero, nell'algebra comune, (x + 7y) (x - 7y) = x2 - 49y2, ma nel modulo 50, - 49 è equivalente a 50 - 49, cioè 1. Perciò x2 - 49y2 = x2 + y2 ≡ 0. Segue che se 12 = 1 e 72 = 49, allora 1+ 49 = x2 + y2 = (x + 7y) (x - 7y) ≡ 0. Analogamente, nel passare dalla serie t50 = 1 + 49 = 50 ≡ 0 alla serie t626 = 1 + 625 = 626 ≡ 0, si arriva al modulo 626. In questo modulo, il numero - 1 ha una radice quadrata che è 25. Nella serie dei naturali fino al 25, si trova che la somma è t = 1 + 25 = 26 ≡ 0:   In questa serie, la coppia centrale è (13,13), e perciò il maggiore dei prodotti è 13x13 = 169. Si prenda allora in considerazione la serie dei naturali fino 169, vale a dire il modulo 170. Qui, nel modulo 170, il numero - 1 ha una radice quadrata che è esattamente 13. Effettivamente 132 + 12 = 170 ≡ 0.   In questa serie, la coppia centrale è (7,7) e perciò il maggiore dei prodotti è 7x7 = 49. Si prenda allora in considerazione la serie dei naturali fino al 49, vale a dire il modulo 50. Qui, nel modulo 50, il numero - 1 ha una radice quadrata che è esattamente 7. Effettivamente 72 + 12 = 50 ≡ 0.

Tra le due successioni vi è una differenza significativa. Se in quella dei naturali fino al 13 il massimo intero il cui quadrato non supera l'ultimo numero è 3, qui, nella successione dei naturali fino al 49, il massimo intero il cui quadrato non supera l'ultimo numero è 7.

Ne segue che, nella prima successione i numeri composti che cadono dal setaccio sono i multipli del 2 e del 3, nella successione dei naturali fino al 49, invece, il procedimento di setacciatura si deve estendere fino a comprendere i multipli del 5 e del 7.

Segue che, una volta che siano caduti i numeri 24,40,48, ossia i multipli del 2 (evidenziati in verde), e i numeri 33 e 45, cioè i multipli del 3 (evidenziati in giallo), in mancanza dei multipli del 5, il prodotto successivo non può che essere il risultato di una coppia di primi: 49 → (7,7):

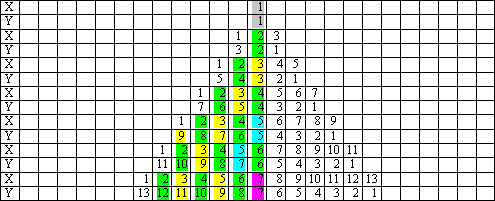
Se il numero 49 non fosse il prodotto di una coppia di primi, la caduta dei numeri composti della successione fino al 50 dipenderebbe esclusivamente dai primi 2 e 3 e tale dipendenza è in contrasto con l'ordinamento dei naturali su cui si fonda il principio del Crivello.

La figura seguente riproduce le prime sette serie in cui i componenti di coppia sono stati evidenziati in relazione al più piccolo dei divisori primi (i multipli del 2 evidenziati in verde; i multipli del 3 in giallo; i multipli del 5 in azzurro; i multipli del 7 in fucsia):

Mediante simili esempi, si può dimostrare che le coppie di primi sono presenti su tutte le infinite serie. Si torni a considerare la serie Δ x + Δ y = t₅₀. Quando dai numeri della somma si passa ai risultati dei prodotti, dalla serie dei naturali fino al 50, si arriva alla serie fino al 626. Il numero dei numeri composti si accresce e passa dai multipli del 3,5,7, ai multipli del 3,5,7,11,13,17,19,23. Segue che una volta caduti i multipli dei multipli del 2, del 3, del 5, del 7, i restanti prodotti si costituiscono come altrettante coppie di primi:

Dovrebbe essere evidente che, se i numeri 481 e 589 non fossero i prodotti di due coppie di primi, la caduta dei composti della successione fino al 626 dipenderebbe esclusivamente dai primi 2,3,5,7, e tale dipendenza è in contrasto con l'ordinamento dei naturali.

D'altra parte, la formazione delle coppie dei primi, in piena coerenza con la definizione costruttiva, è connessa alla legge di conservazione delle coppie dei fattori comuni. In questo caso, come si è già visto, i numeri composti cadono dal setaccio in corrispondenza dei primi 3,5,7. Fra questi primi solo il 5 divide somme e prodotti e perciò solo questo numero può formare dei multipli dei suoi multipli. Segue come logica conseguenza che, i primi che restano nel setaccio (tra cui 3 e 7), poiché non possono formare dei multipli con i loro multipli, per formare delle coppie, devono necessariamente combinarsi con altri primi: (3,47),(7,43), (13,37), (19,31).