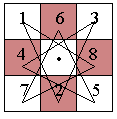
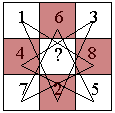
(Un problema di teoria dei grafi) Gabriella C. Zammillo Abstract Il salto del cavallo è un importante problema traducibile sia in termini di grafi euleriani che in termini di grafi hamiltoniani. Con questo articolo, oltre a voler sottolineare il valore del gioco nella didattica della matematica, si presenta il problema e si esaminano le sue possibilità di soluzione. Si comprende quindi perché si può disegnare un cammino chiuso, in cui tutte le possibili mosse siano tracciate una sola volta soltanto, nel caso in cui il cavallo si muove su una scacchiera n×n con n=3; perché il cavallo può occupare tutte le caselle di una scacchiera n×n ritornando sulla casella da cui è partito solo nel caso n×n con n ³ 6 e pari; perché nel caso n×n con n=5 il cammino non è chiuso ed inoltre quanti possibili cammini chiusi può descrivere il cavallo muovendosi su di una scacchiera n×n con n pari. Introduzione Che il gioco stimolasse la fantasia è cosa nota, ma che questo, presentato sotto forma di rompicapi e indovinelli risultasse un utile strumento d'apprendimento nella didattica della matematica forse lo è un po' meno, sebbene siffatti argomenti ricreativi avessero catturato l'interesse di grandi menti matematiche da Eulero a Leibniz, da Hilbert ad Einstein ed alcune teorie matematiche avessero avuto origine proprio dall'analisi e discussione di rompicapi. È il caso della Teoria dei Grafi [B1] - [F1] - [O1] le cui origini risalgono al 1736 quando Eulero riuscì a spiegare l'impossibilità di soluzione del "problema dei sette ponti di Könisberg", tormento di non poco conto per gli abitanti dell'antica cittadina prussiana. Ma se " i sette ponti di Könisberg" rappresentano un importante problema di teoria dei grafi, non è certo da meno, sebbene sia poco conosciuto, pur essendo stato trattato da Eulero già nel 1759 e poi da Legendre, Vandermonde ed altri, "il salto del cavallo sulla scacchiera". Ebbene, in questo articolo, tratto dalla mia tesi di laurea dal titolo "La passeggiata di Eulero sui sette ponti e i viaggi di Hamilton su un dodecaedro" [Z1], concepito con l'intento di sottolineare il valore del gioco nella didattica della matematica, si è cercato di presentare alcuni aspetti del problema e le relative soluzioni con un linguaggio accessibile anche ai non addetti ai lavori che pure abbiano qualche interesse all'argomento rimandando per gli approfondimenti ai testi ed agli articoli citati in bibliografia. È noto dalle regole del gioco degli scacchi che il cavallo salta sulla scacchiera spostandosi lungo la diagonale di un rettangolo composto da 3×2 caselle passando da una casella bianca ad una nera o viceversa come mostrato in fig.1.1.
Allora:
Esprimiamoci in termini di teoria dei grafi. Intuitivamente con la parola "grafo" intendiamo una struttura che ci permette di rappresentare gli elementi di un insieme e una relazione tra tali elementi detti rispettivamente "vertici" e "spigoli", in altre parole: DEF.: Diciamo "grafo" una coppia ordinata (V(G), E(G)) tale che V(G) è un insieme non vuoto ed E(G) è un insieme di coppie non ordinate di elementi di V(G). Pertanto, nel nostro caso specifico, i vertici sono rappresentati dai quadrati della scacchiera mentre gli spigoli dalle mosse del cavallo identificando ogni mossa con la coppia (casella di partenza, casella d'arrivo) e poiché una sequenza alternata di vertici e spigoli definisce un "cammino", possiamo cimentarci nel risolvere un problema più complesso che chiede:
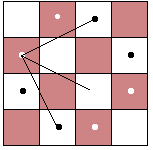
Si capisce bene che in base alle definizioni date di vertice e spigolo, i termini mosse e caselle consentono di tradurre il problema del "salto del cavallo" rispettivamente in termini di "grafi euleriani" ed in termini di "grafi hamiltoniani". E allora, ispirandoci a quanto fatto da Eulero col problema di Könisberg, rispondiamo al primo quesito. 1. UN PROBLEMA DI CAMMINI EULERIANI Il primo quesito riformulato, chiede in sostanza se è possibile costruire un cammino euleriano nel grafo. Ribadiamo, a tal proposito, che un "cammino" è una sequenza finita ed alternata di vertici e spigoli; che un cammino è "chiuso" quando il primo e l'ultimo vertice sono coincidenti e che un cammino è detto "euleriano" quando oltre ad essere un cammino chiuso, la sequenza che lo individua contiene ogni spigolo del grafo una ed una sola volta mentre, al contrario, è detto cammino "semi-euleriano" quando, pur contenendo ogni spigolo del grafo una ed una sola volta, esso risulta non chiuso. Inoltre, con la sua ben nota condizione necessaria e sufficiente, Eulero ci insegna che affinché in un grafo sia possibile costruire un cammino euleriano, tale grafo deve avere tutti i vertici di grado pari o se vogliamo costruire invece un cammino semi-euleriano, il grafo considerato deve contenere al massimo due vertici di grado dispari dove per grado si intende il numero di spigoli uscenti dal vertice dato. In virtù di quanto appena richiamato, torniamo alla nostra scacchiera. È evidente che una risposta affermativa al problema prima esposto la si ha soltanto se il cavallo si muove su di una scacchiera n×n con n=3 infatti è soltanto in questo caso, la fig.1.2 ci aiuta a comprendere il motivo, che tutte le caselle occupate dal cavallo consentono due mosse: una in entrata, l'altra in uscita.
Ciò vuol dire che ogni singolo vertice contenuto nel grafo tracciato ha grado 2 quindi, poiché è soddisfatta la teoria di Eulero, il cammino disegnato è proprio quello richiesto. È altresì chiaro che la condizione di Eulero non potrà essere verificata per n > 3 infatti già in una scacchiera 4×4 esistono otto caselle dalle quali sono possibili 3 mosse (cfr. fig.1.3), cioè il cavallo non potrà uscire da una di queste caselle dopo esservi entrato la seconda volta (cfr.fig.1.4).
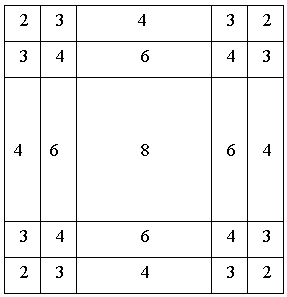
L'esistenza di un numero maggiore di 2 di siffatte caselle e quindi l'esistenza di un numero maggiore di 2 di vertici di grado dispari contraddice ovviamente il teorema di Eulero ragion per cui il problema, già a partire da una scacchiera 4×4 per poi essere generalizzato ad una n×n, non potrà mai avere soluzione proprio perché le otto caselle di grado dispari non solo continueranno ad esistere, ma continueranno anche ad essere adiacenti alle quattro caselle di grado 2 poste ai rispettivi quattro angoli della scacchiera (cfr.fig.1.5).
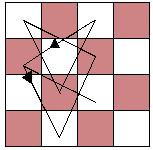
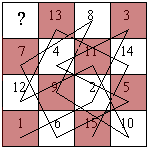
2. UN PROBLEMA DI GRAFI HAMILTONIANI Chiedere se sia possibile muovere il cavallo su una scacchiera n×n occupando tutte le caselle esattamente una volta equivale a risolvere invece un problema di cammini hamiltoniani. Questione abbastanza delicata e tra l'altro tuttora aperta, quella dei cammini hamiltoniani, ma nel nostro caso ci avvaliamo del contributo dovuto a Conrad, Hindrinchs, Morsy e Wegener [C1] risalente al 1994 e contenente efficienti algoritmi per la costruzione dei cammini hamiltoniani. Tradurre il problema in termini di grafi hamiltoniani significa chiedere se esiste nel grafo considerato un cammino chiuso detto "ciclo hamiltoniano" che contiene ogni vertice del grafo una ed una sola volta oppure un "cammino hamiltoniano" se il cammino dovesse risultare non chiuso pur contenendo sempre ciascun vertice una ed una sola volta. È ovvio che nessuno dei due cammini potrà mai esistere nel caso in cui la scacchiera sia una 3x3 oppure una 4x4 perché il numero ridotto di caselle impedisce al cavallo di occuparle tutte con una ulteriore mossa. Com'è facile notare in fig.2.1, in entrambi i casi sono state tracciate tutte le possibili mosse del cavallo, ma su nessuna delle due scacchiere è stato possibile descrivere il cammino richiesto.
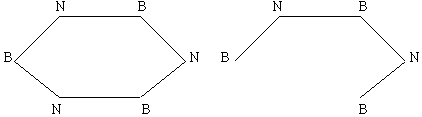
Tuttavia osserviamo che data una sequenza alternata di caselle bianche e nere come in fig.2.2, sarà possibile costruire un ciclo hamiltoniano che le contenga tutte e alternativamente, una bianca ed una nera, solo nel caso in cui il loro numero sia pari, perché se fosse altrimenti, verrebbero ad essere adiacenti due caselle dello stesso colore contraddicendo le ipotesi.
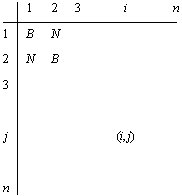
È proprio sulla base di questa osservazione che si fonda il "criterio del colore" formulato da Conrad e gli altri per poter ammettere l'esistenza di un "cammino hamiltoniano", criterio secondo il quale un cammino hamiltoniano, da una casella contrassegnata s ad una casella contrassegnata t e distinta da s, esiste per n ³ 6 se e soltanto se n è pari ed s e t hanno colore differente oppure n è dispari, ma s e t hanno colore bianco (supposto che agli angoli della scacchiera ci siano caselle bianche). Dato quindi il grafo Gn come la coppia Gn = (Vn, En) definita in precedenza, rappresentiamo la scacchiera n×n, per la quale si considera il grafo Gn, attraverso un sistema di riferimento come mostrato in fig.2.3 in cui le coppie (i, j) con 1 £ i, j £ n individuano le caselle e indichiamo con c la funzione colore tale che: c : (i, j)® c(i, j) = bianco se i+j è pari
Posto allora: c(s) = c(is, js)
Conrad definisce il "criterio del colore" per una generica n×n con:
c(s) = c(t) = bianco se n è dispari
e prova il seguente teorema: TEOREMA
ii)Sia n=5.
Alla soluzione ci si arriva attraverso un efficiente algoritmo detto "backtracking algorithm" applicato ad un numero finito di casi speciali tra cui anche a problemi su scacchiere rettangolari e non-rettangolari. Solo successivamente si ricorre alla strategia definita del "dividere e sormontare ostacoli". La scacchiera n×n viene cioè suddivisa in sottoscacchiere più piccole così che il problema su una siffatta sottoscacchiera può essere risolto con più rapidità ed in maniera tale che le soluzioni di questi piccoli problemi possano poi essere combinate tra loro e costituire la soluzione per il problema più generale. Al teorema segue un corollario. COROLLARIO: Gn contiene un ciclo hamiltoniano Û n ³ 6 con n pari. Dim.: È ovvio che per n £ 4 il grafo non conterrà mai un "ciclo hamiltoniano" perché l'esistenza di un siffatto cammino proverebbe l'esistenza di un "cammino hamiltoniano" contenuto in esso e ciò sappiamo essere assurdo. Il "ciclo hamiltoniano" non sarà contenuto nel grafo neanche per n dispari perché, se un siffatto ciclo esistesse, i vertici iniziale e finale avrebbero colore differente contro la definizione di ciclo. Il corollario è provato solo per n ³ 6 e pari infatti, tracciato un cammino hamiltoniano dalla casella contrassegnata (1,1) alla casella contrassegnata (2,3), tale cammino assieme alla mossa dalla casella (2,3) alla casella (1,1) definisce il ciclo hamiltoniano richiesto. In virtù di quanto detto finora possiamo enunciare il seguente teorema: TEOREMA: Il cavallo, saltando su una scacchiera n×n, può occupare tutte le caselle ciascuna esattamente una volta descrivendo un cammino hamiltoniano Û n ³ 5. Si vedano le soluzioni per le scacchiere 5×5, 6×6, 12×12 in fig. 2.4 e fig. 2.5.
Forse potrebbe apparire provocatorio chiedere di determinare il numero dei possibili cicli hamiltoniani descritti da un cavallo mosso su di una scacchiera n×n con n pari, ma se simili provocazioni sono utili a stimolare la creatività e la fantasia, se servono ad alimentare la sfida attraverso cui misurare le proprie capacità, allora ben vengano e vediamo a quali risultati hanno portato Kyek, Parberry e Wegener [K1] nel 1997. Il numero richiesto è ovviamente uguale a 0 per n = 2 ed n=4, pari invece a 9862 per n=6. Per n=8 il miglior limite inferiore trovato (risultato dovuto a Kraitschik nel 1953) è pari a 122802512. In realtà sembra impossibile poter determinare il numero richiesto per n in generale. Grazie alle ricerche condotte da Kyek, Parberry e Wegener possiamo conoscere un limite superiore trovato per il particolare caso n=8 che viene stimato in 3.019 x 1022 possibilità. Studiando il comportamento asintotico di questi valori, segue che il numero Fn dei cicli hamiltoniani che il cavallo può descrivere su una scacchiera (per n pari) è limitato superiormente da LEMMA: Sia G un grafo con n vertici ed m spigoli. Sia scelto kÎN tale che (n-1)[m/(n-1)] + k = m allora il numero di cammini hamiltoniani che hanno inizio da un qualsiasi vertice v è limitato superiormente da: [m/(n-1)]n-1-k [m/(n-1) +1]k Si osserva che il numero dei "cicli hamiltoniani" è al più la metà del numero dei "cammini hamiltoniani" che hanno inizio da un qualsiasi vertice. Il grafo descritto dal cavallo su una scacchiera 8×8 ha 168 spigoli per cui il limite superiore ottenuto per il numero di cicli hamiltoniani su una siffatta scacchiera è (1/2)221342 £ 1.148 x 1026. Tale limite superiore ( per il particolare caso n=8) è stato tuttavia notevolmente migliorato infatti, attraverso l'uso di un calcolatore, studiando i differenti casi a cui le possibili mosse danno luogo ed esaminando i cammini di diversa lunghezza di conseguenza costruiti, si ottiene il seguente risultato: TEOREMA.: Il numero di cicli hamiltoniani tracciati da un cavallo mosso su di una scacchiera 8×8 è al più pari a Fn = 3.019 × 1022. Ricorrendo alla tecnica del "dividere e sormontare ostacoli", sappiamo che è possibile costruire differenti cicli hamiltoniani su di una scacchiera n×n suddividendo questa in sottoscacchiere. Supponiamo che dalla suddivisione si ricavino sottoscacchiere di dimensione 6×6, 6×8, 8×6 ed 8×8. Scelto a Î [0,1/6] si ottengono pertanto a2n2 bordi di dimensione 6×6, (1/8)a(1-6a)n2 bordi di dimensione 6×8 ed 8×6 mentre (1/64)(1-6a)2n2 bordi di dimensione 8×8. Poiché a noi interessa stimare il numero dei differenti cammini hamiltoniani all'interno di tali sottoscacchiere, utilizzando i risultati raggiunti da Kyek e gli altri con l'aiuto di un calcolatore, osserviamo che relativamente al caso di una sottoscacchiera 8×8 esistono almeno M8,8=19.610.000 cammini hamiltoniani, per una 6×6 abbiamo M6,6=44670 mentre per una 6×8 ed 8×6 il numero è pari a M6,8=M8,6=1.800.000. Il limite inferiore per il numero di cicli hamiltoniani è così pari a :
Tale limite assume il suo valore massimo per a=1/6. Poiché la partizione in bordi da 6×6 consente di ottenere il miglior limite inferiore in quanto M6,6 rappresenta il valore stimato con più precisione rispetto agli altri, risulta che il limite inferiore per a=1/6 è uguale a :
e segue che: TEOREMA.: Il numero di cicli hamiltoniani descritti su di una scacchiera n×n è pari a Fn=W(1.3535 n2). Bibliografia [B1] J.A. Bondy - U.S.R. Murty: Graph theory with application, The Mac Millan Press LTD, Hong Kong 1976
| ||||||||||||||||||||||