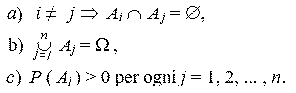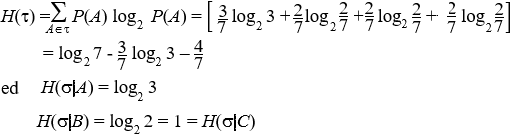Mauro Cerasoli Appunti di un seminario tenuto da Gian Carlo Rota a L'Aquila nel maggio 1990. 1. Introduzione Viene estratta a caso una pallina da un'urna che ne contiene una bianca ed una rossa. Quale pallina uscirà? Nessuno è in grado di rispondere a questa domanda. Se però l'urna ha tre palline bianche e dieci rosse, siamo tutti disposti a scommettere sull'uscita di una pallina rossa. In questo secondo caso è diminuita l'incertezza rispetto all'esito dell'altra estrazione. Se, infine, l'urna ha mille palline di cui una sola bianca e tutte le altre rosse, ogni persona ragionevole sarà disposta a scommettere che questa volta uscirà quasi certamente una pallina rossa. L'incertezza è scomparsa: in altre parole possiamo dire che le tre urne danno informazioni crescenti rispetto a ciò che accadrà: il variare della composizione dell'urna determina la variazione dell'incertezza. E' possibile misurare in qualche modo l'incertezza? La risposta è affermativa ed il concetto adeguato allo scopo è quello di entropia, introdotto da C. E. Shannon nel suo lavoro pionieristico The mathematical theory of communications pubblicato nel 1948 sul Bell Syst. Tech. Journal, 27, pp. 379-423 e 623-656. Prima di presentare gli assiomi che caratterizzano l'entropia, conviene richiamare alcuni concetti di calcolo delle probabilità necessari per capire quanto esporremo in seguito.
Se le variabili aleatorie X e Y sono indipendenti, anche tX e tY sono indipendenti. 2. Assiomi dell'entropia Teorema. Dato uno spazio di probabilità (W, F, P) esiste una sola funzione H, detta entropia, H: P*®R, tale che:
L'unica funzione H che soddisfa gli assiomi precedenti è
Prima di dimostrare questo teorema osserviamo che solo l'assioma e) necessita di qualche chiarimento: illustriamolo con un esempio relativo ad un classico problema di pesate. Abbiamo in mano tre monete a, b, c; si sa che almeno una è buona, cioè più pesante. Con una bilancia a due piatti vogliamo individuare quali monete, se ci sono, sono false. Lo spazio campione W del problema consiste di sette punti, ciascuno per ognuna delle possibilità di monete buone. Così se W = {a, b, c, ab, ac, bc, abc}, siamo in presenza della partizione minima s = 0^. Ora che cosa succede quando mettiamo la moneta a sul piatto a sinistra e la b sul piatto a destra della bilancia? Lo spazio W si spezza in tre alternative corrispondenti ai tre possibili esiti della pesata:
L'entropia di s = 0^ è log2 7 mentre
e quindi Risulta Con una pesata, cioè con l'informazione avuta da essa, abbiamo ridotto l'incertezza passando da un'entropia H(s)=log27 ad un'entropia minore Dopo aver registrato il risultato della pesata, mettiamo la terza moneta al posto della prima. L'esito della seconda pesata partiziona ciascuna alternativa di t nel modo seguente:
L'informazione combinata delle due pesate ci permette di individuare l'alternativa della partizione s corrispondente alla reale situazione di monete false e buone. Ora s è più fine di t e l'assioma e) vuol dire che l'entropia di s è quella di t più una media pesata, con le alternative A dit, dell'entropia condizionata di s ad A. Procediamo allora dimostrando dapprima il Lemma di Erdos. Se la partizione t ha n alternative di uguali probabilità, allora H(t ) = log2 n. Consideriamo il caso in cui la partizione t ha k alternative equiprobabili e s ne ha kn, sempre tutte equiprobabili. Per ipotesi, quindi, P(A) = 1/k per ogni A Î t e P(B) = 1/(kn) per ogni B Î s. L'entropia H dipende dunque da k e n mediante una funzione, diciamo f, e sarà Se A è un'alternativa di t, per l'assioma e) risulta Inoltre, per l'assioma H(1^) =0, deve essere f(1) =0, mentre per l'assioma c) deve risultare f(2) = 1. L'unica funzione f che soddisfa tali proprietà è f(n) = log2 n. Analizziamo ora il caso in cui la partizione t ha due alternative A e B mentre s ha n alternative ottenute dividendo A in k alternative e B in n-k alternative, tutte di probabilità 1/n. Per quanto dimostrato poco fa, risulta H(s) = log2 n, H(s | A) = log2 k, H(s ú B) =log2 (n-k) quindi dall'assioma e) otteniamo 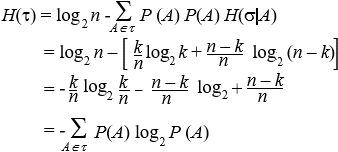 In particolare, se t = {A, B} con P(A) = p, P(B) = 1- p, allora Quando la partizione t = {A, B, C} ha tre alternative, sia s = {A, B È C}. Essendo ora t £ s risulta di conseguenza 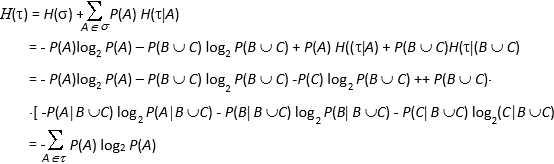 Procedendo per induzione si dimostra la (2.1). 4. Proprietà dell'entropia Teorema. La funzione di entropia H soddisfa le seguenti proprietà:
La proprietà a) è ovvia dalla formula (2,1); la dimostrazione di b) necessita della disuguaglianza
dove l'uguaglianza si ha solo per x = 1. Ponendo x = 1/n P(A) abbiamo  Pertanto ma, come sappiamo dal lemma di Erdos, log2 n corrisponde all'entropia di t con alternative equiprobabili. Per dimostrare c) si consideri la funzione y = x log2 x, convessa per x > 0. Allora, se li > 0, l1 + l2 + ...+ ln = 1, risulta la disuguaglianza Possiamo quindi scrivere 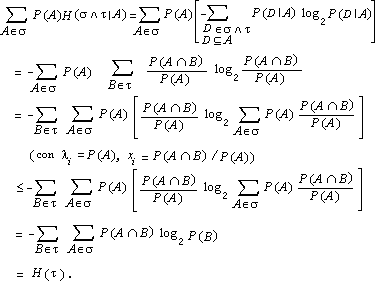 Perciò, essendo s Ù t £ t, si ha per l'assioma e) Dimostriamo infine la d); se s e t sono indipendenti allora P(A Ç B) = P(A) P(B) per ogni A Î s e B Î t, quindi 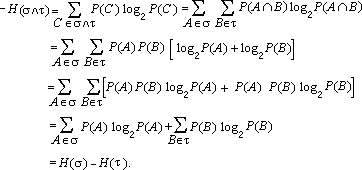 5. L'entropia nel continuo Se X è una variabile aleatoria discreta con distribuzione di probabilità pk, si definisce entropia di X il numero Questa serie è convergente in quanto e l'ultima serie converge perché pk2 £ pk . Se invece X è una variabile aleatoria continua con densità f X (x), la sua entropia (detta di Boltzmann) H(X) è definita dall'integrale dove il logaritmo è in una base qualsiasi (per esempio 2). Le variabili aleatorie uniformi su [0, a], esponenziale di parametro a, e normale di media m e deviazione standard s hanno entropia rispettivamente uguali a log a, 1 - log a, log s Ö(2pe). Queste tre variabili aleatorie godono di una particolare proprietà di massimo rispetto all'entropia. Infatti si può dimostrare il seguente Teorema dell'entropia massima. Tra tutte le variabili aleatorie continue a valori
quelle con entropia massima sono la
Ci limitiamo a dimostrare solo i casi a) e b) essendo c) reperibile sui testi classici di teoria dell'informazione. Se f(x) è una qualsiasi densità sull'intervallo [0, a] allora 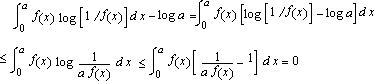 Quindi ma log a è l'entropia della densità uniforme su [0, a]. Allo stesso modo, per una variabile aleatoria X con densità f(x) definita su [0, ¥[ e di media 1/a, consideriamo la disuguaglianza  L'uguaglianza si ha solo per f(x)=a e -a x ; in tal caso risulta H(X ) £ 1- log a ma 1 - log a è l'entropia della densità esponenziale di parametro a. |