1 - Origini del metodo Monte Carlo.

Una particella veloce colpisce in pieno il nucleo di un atomo. Questo si frantuma in molte particelle, che vanno a colpire i nuclei di altri atomi vicini, che si frantumano a loro volta, secondo una reazione a catena, nel corso della quale si libera una gran quantità d'energia. Il processo durerà fino a coinvolgere l'intero universo o s'arresterà, dopo un certo numero di reazioni? Sappiamo già che il secondo caso è quello che ci si attende, come è stato confermato sperimentalmente dai fisici. Con quale stato d'animo fu tuttavia possibile eseguire il primo esperimento? I fisici erano certi del fatto che la reazione avrebbe avuto termine?

In realtà, l'esperimento fisico fu preceduto da una serie di simulazioni. Una volta introdotti alcuni parametri iniziali, il fenomeno fu simulato da un calcolatore per mezzo di valori casuali, trattati con metodi statistici.
Si poteva così stimare la probabilità che, dopo un certo numero di "generazioni", le particelle emesse nel corso delle reazioni a catena, cessassero di generare altre particelle. Le simulazioni dettero sufficienti garanzie e gli esperimenti reali furono eseguiti con una buona dose di tranquillità
Fu Enrico Fermi, a detta di Emilio Segré, ad inventare il metodo Monte Carlo (senza usare questo nome), quando studiava a Roma il moto dei neutroni all'inizio degli anni 30.
Stanislaw Ulam usò il metodo Monte Carlo nel '46. Narra egli stesso: "... L'idea del metodo Monte Carlo mi è venuta giocando a carte un solitario durante un periodo di convalescenza, nel 1946. Avevo sprecato un mucchio di tempo per calcolare, senza successo, con tecniche combinatorie, la probabilità di riuscita del solitario. Pensai allora che, giocando un centinaio di volte il solitario, avrei potuto stimare questa probabilità con la frequenza delle volte con cui era riuscito, aggirando così con la pratica il pensiero astratto. Questo metodo era ormai possibile, visto l'avvento dei calcolatori veloci.
Era ovvio pensare anche a soluzioni simili per problemi legati alla diffusione dei neutroni o di fisica matematica e, più in generale, a come scambiare processi descritti da certe equazioni differenziali con un modello equivalente interpretabile come successione di operazioni aleatorie. In seguito descrissi l'idea a John von Neumann e cominciammo a realizzare veri e propri calcoli matematici al riguardo."
Sono tanti ormai i campi in cui si utilizzano metodi statistici per ottenere informazioni e stime su fenomeni legati al caso. Non occorre che i dati siano raccolti durante un esperimento reale in cui tali fenomeni avvengono. Ciò potrebbe richiedere troppo tempo e, in ogni caso, non sempre la natura è disposta a fornirci situazioni aleatorie ... a comando. I dati possono allora provenire da simulazioni fatte per mezzo di un computer, in grado di generare sequenze di numeri casuali. Esse sono quindi utilizzate per simulare per migliaia di volte il fenomeno aleatorio, raccogliendo così rapidamente una serie di dati che, trattati con metodi statistici, forniscono stime che diventano tanto più attendibili quanto più è grande il numero delle prove fatte.

 2 - Il metodo Monte Carlo nella didattica.
Il metodo Monte Carlo, può essere usato a scuola per agevolare lo studio dei fenomeni aleatori e raffrontare i risultati ottenuti dalle simulazioni con il computer, con quelli dettati dalla teoria. Si vedrà che i risultati empirici s'avvicinano tanto più a quelli teorici quanto maggiore è il numero delle prove fatte.
Dal punto di vista didattico, si ottiene un importante risultato. Si accresce negli allievi il grado di fiducia sull'efficacia dei metodi statistici. Si dà loro un'idea più consapevole del concetto di evento fortuito, e si evitano così alcune difficoltà concettuali che essi incontrano durante le fasi iniziali nell'apprendimento della matematica dell'incerto. Essi riescono così a comprendere meglio il concetto di probabilità di un evento, assegnando ad essa il valore di grado d'attendibilità nella previsione di fenomeni aleatori.
Qual è il significato che può essere attribuito, infatti, alla probabilità assegnata ad un determinato evento? Non è certo quello di stabilire a priori se il fenomeno accadrà o no nel corso di un singolo esperimento. Tuttavia, quando l'esperimento è ripetuto più volte in condizioni di uniformità, le cause assolutamente imprevedibili che ne determinano i vari esiti, sembrano piegarsi man mano ad un ordine razionale. E' come se il fenomeno aleatorio obbedisse a leggi che appaiono molto vicine a quelle di tipo deterministico, con cui spesso si descrivono molti fenomeni del mondo fisico. E' proprio ricorrendo a modelli di tipo probabilistico, che alcuni fenomeni naturali hanno trovato interpretazioni accettabili. Dopo alcune perplessità iniziali, (A.Einstein: "Dio non gioca a dadi..." ) si sono moltiplicati i tentativi di applicare modelli probabilistici ad un numero sempre più grande di fenomeni naturali. I fenomeni della realtà si vanno rivelando, infatti, sempre meno legati ai modelli deterministici che l'uomo ha finora cercato di proporre, per seguire piuttosto modelli di tipo probabilistico, che occorre imparare a comprendere e ad interpretare. E' quindi ampiamente giustificata l'introduzione di tali modelli nella didattica della matematica e delle scienze.
Il metodo Monte Carlo permette di ottenere con relativa facilità i risultati in situazioni anche molto complesse. Essi sono spesso approssimati e contengono un grado d'incertezza (piccolo, quanto si vuole, ma non eliminabile). Tali risultati sono tuttavia resi molto attendibili dalle leggi matematiche alle quali il processo è sottoposto. Ci riferiamo, in particolare, della legge dei grandi numeri o legge empirica del caso, che lega strettamente i risultati statistici con la teoria della probabilità.
Parlare di fenomeni aleatori o di risultati approssimati ed incerti, comporta indubbiamente un salto di mentalità abbastanza notevole nella matematica. In tale campo sembrano avere cittadinanza solo risultati certi, ottenuti attraverso rigorosi processi logici, in cui nulla è lasciato al caso. L'uso dei metodi statistici, favorito dall'avvento del computer, apre il campo ad un settore della matematica che potremmo definire sperimentale e che si presenta per molti aspetti rivoluzionario rispetto ad abitudini consolidate da una tradizione millenaria. Sono perciò comprensibili, ma sempre meno accettabili, le reazioni negative che tali innovazioni suscitano spesso in molti matematici dall'impostazione classica. Le simulazioni per mezzo del computer vanno sempre più sostituendosi ai metodi analitici, specialmente in settori nei quali si chiede alla matematica di fornire risposte immediate a problemi concreti, a prescindere da quanto ne pensino in proposito i matematici rigorosi.

 3 - Alcuni esempi concreti di applicazione didattica del metodo Monte Carlo.
E' il momento di passare ora all'esame di una serie di proposte e di suggerimenti concreti sul modo di applicare i concetti fin qui sviluppati, nella didattica della matematica dell'incerto.
A tal fine è stato realizzato un pacchetto di 22 programmi, che serviranno a simulare fenomeni aleatori di vario genere, dei quali illustriamo la natura e diamo qualche suggerimento sul loro uso didattico.
Si partirà da problemi dei quali è già nota la soluzione, per lo più di tipo combinatorio (lancio di monete, dadi, ecc.) Nel corso della simulazione si fisserà il numero di prove che si desidera effettuare. Sarà bene iniziare con un piccolo numero di prove, per poi passare ad un numero sempre più grande, in modo da verificare la tendenza dei dati a stabilizzarsi intorno a determinati valori, che sono poi quelli previsti dalla teoria.
Si affronteranno poi problemi di difficile soluzione, almeno per il grado di conoscenze degli alunni (in alcuni casi, anche rispetto al grado generale di conoscenze). In tal modo si potrà apprezzare l'uso del computer che, per mezzo di prove ripetute, ci offrirà almeno una misura approssimata della probabilità che ha il fenomeno di verificarsi. In alcuni esempi il risultato approssimato appare in tempo reale durante l'esperimento stesso, permettendo di verificare direttamente la progressiva stabilizzazione delle sue cifre, all'aumentare del numero di prove. In tal modo l'allievo sarà stimolato a dare egli stesso, nel corso dell'esperimento, una sua personale valutazione circa il valore che si otterrà al termine. Il raffronto dei valori stimati con quelli teorici, previsti dal calcolo delle probabilità (che in genere sarà comunicato alla fine), sarà molto più efficace di ogni discorso, circa la natura dei fenomeni aleatori e le stime sulla loro probabilità di verificarsi.
Il lavoro terminerà con alcuni esempi in cui o non è nota la soluzione dei problemi proposti, oppure si conosce la procedura per arrivare ai risultati, ma essa è talmente complessa da renderli praticamente inaccessibili. Si resterà talvolta un po' sorpresi del grado di difficoltà presentato da alcuni problemi, vista la semplicità della loro enunciazione. In ogni caso il computer ci fornirà la soluzione, o meglio, un suo valore stimato, ma attendibile. Siamo consapevoli del fatto che si tratta di una soluzione approssimata, ma sappiamo ormai, grazie alle esperienze precedenti, che la sua approssimazione rispetto al valore cercato dipenderà solo dal numero di prove fatte.
I pochi esempi proposti saranno sufficienti a far intuire le numerose possibilità di applicazione dei metodi proposti.

 4 - Lancio di due dadi.

Si lanciano due dadi e si vogliono trovare le probabilità dei vari esiti, costituiti dalle varie somme che si possono ottenere. Il problema è ben noto e la sua soluzione è semplicissima. Basta costruire una tabella a doppia entrata con i 36 possibili esiti delle somme dei due dadi. Le somme vanno da un minimo di 2 ad un massimo di 12. Le probabilità dei vari esiti sono date dai rapporti tra i rispettivi casi favorevoli (1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1) e il totale dei 36 casi possibili. Il computer serve come primo approccio all'uso dei metodi statistici, in quanto permette di determinare facilmente le frequenze relative, al variare del numero di lanci. Una volta introdotto il numero di lanci, il programma procede a calcolare le frequenze relative (rapporto tra il numero dei casi in cui si verifica un esito rispetto al numero totale di prove effettuate), fornendo al termine una tabella con i risultati ed i raffronti rispetto ai relativi valori teorici.

E' consigliabile eseguire più volte il programma, partendo da un piccolo numero di lanci. Si eseguono poi prove con un numero di lanci sempre maggiore. La tabella, che compare ogni volta, fornirà gli opportuni raffronti fra le frequenze relative ottenute con il computer e le rispettive probabilità.

 5 - Lancio di n monete.

Si lanciano n monete e poi si conta il numero di teste. I possibili esiti vanno da un minimo di zero teste, fino ad un massimo di n. Per consentire la visualizzazione dei risultati sullo schermo, il numero n non deve superare 10. Le probabilità di ogni esito si possono calcolare per mezzo della combinatoria. I casi favorevoli sono dati dai coefficienti binomiali ( nk ) con n numero monete lanciate e k numero di teste. I casi possibili sono 2n. Ad esempio, lanciando 5 monete, la probabilità che escano esattamente 3 teste è (53)/25 = 10/32.

Il computer provvederà ad effettuare i lanci, trovando le frequenze relative dei vari esiti e le rispettive probabilità.

 6 - Modello di Ehrenfest.

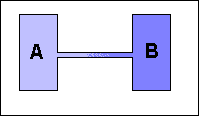Nel 1907 i coniugi Paul e Tatiana Ehrenfest pubblicarono su "Physik Zeitschrift" un articolo, proponendo il seguente modello probabilistico per spiegare il fenomeno della diffusione dei gas. Si collegano tra loro due recipienti A e B, contenenti molecole di gas a differente pressione. Si suppone che, ad ogni istante, una molecola scelta a caso passi da un recipiente all'altro. Naturalmente è più probabile che la molecola sia scelta tra quelle del recipiente che ne ha di più.

Così facendo però, diminuiscono le molecole nel primo recipiente e quindi si riduce la probabilità che esse passino nel secondo recipiente. In quest'ultimo si verifica il fenomeno opposto. Si stabilisce dopo un po' un equilibrio dinamico in cui i due recipienti hanno la stessa pressione e contengono all'incirca lo stesso numero di molecole, mentre continuano a transitare dall'uno all'altro.
La simulazione al computer prevede due urne (recipienti). L'operatore assegna a ciascuna di esse un certo numero di biglie (molecole di gas). Il programma estrae una biglia a caso. La biglia estratta, passa dalla propria urna all'altra. Si continua così, fino a quando il numero di biglie nelle urne è uguale, cosa che si verifica invariabilmente, anche quando le quantità di biglie, inizialmente assegnate alle due urne, erano sensibilmente diverse tra loro.

 7 - Simuliamo una passeggiata a caso: il quincunx di Galton.

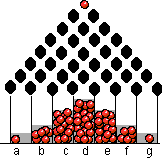Si deve a John Galton un modello per la simulazione di una passeggiata a caso. Una biglia cade lungo un piano inclinato, sul quale sono posti ostacoli che la obbligano a deviare a destra o a sinistra, in modo del tutto casuale. Continuando a scendere, la biglia supererà tutti gli ostacoli e finirà per cadere in una delle celle poste al termine dei vari percorsi. Naturalmente non tutte le celle hanno la stessa probabilità di essere raggiunte dalla biglia che rotola. Il problema ha una stretta analogia con quello del lancio di n monete. Basta riflettere sul fatto che la biglia, nel seguire i vari percorsi, si comporta come se ogni volta lanciasse una moneta: testa, per andare a destra e croce, per andare a sinistra.

Per calcolare le probabilità di passare attraverso i varchi esistenti tra gli ostacoli, si possono quindi utilizzare i coefficienti binomiali già visti nel lancio delle monete, oppure calcolare le successive righe del triangolo di Pascal. Sapendo che la somma dei termini di ogni riga vale 2ⁿ, sarà facile calcolare le probabilità e raffrontarle con le frequenze relative.
Il programma realizzato al computer realizza il movimento delle palline, che cadono dall'alto e, passando attraverso le varie porte, arrivano in una delle celle poste in basso, mentre un grafico ad istogrammi evidenzia le frequenze delle biglie cadute in ciascuna di esse. Al termine sarà possibile visualizzare la solita tabella con il raffronto tra i dati statistici e quelli teorici.
Nel nostro esempio, le probabilità che una biglia finisca in una delle celle contrassegnate con le lettere a, b, c, e, f, g, sono rispettivamente 1/64, 6/64, 15/64, 20/64, 15/64, 6/64, 1/64.

 10 - Selezione darwiniana.
Molte specie di animali (pesci, anfibi, insetti, ecc.) mettono al mondo un altissimo numero di figli. La maggior parte di essi è destinata ad essere eliminata. La fame, le malattie, i predatori ed altri fattori agiscono a caso sulla popolazione, eliminando gli individui in eccesso. Darwin presumeva che gli individui eliminati avessero qualche caratteristica che determinava sin dall'inizio una minore probabilità di sopravvivenza.
Il modello molto semplificato da noi proposto prevede un numero iniziale di 1000 individui che si ridurranno a 50. Gli individui sono divisi in quattro gruppi, con diverse probabilità di sopravvivenza. Le probabilità andranno assegnate prima di iniziare l'esperimento. Non occorre che le probabilità differiscano di molto tra loro. Anzi è interessante il caso in cui esse sono piuttosto vicine, ad esempio, 0.54 - 0.51 - 0.50 - 0.48 . Inizia quindi il processo di selezione, al termine del quale si vedrà quanti sono gli individui sopravvissuti in ciascuno dei quattro gruppi iniziali. Il maggior numero di sopravvissuti apparterranno quasi certamente al gruppo più favorito. Si verificheranno casi di totale estinzione dei ceppi di individui meno favoriti, pur in presenza di piccolissime differenza tra i vari gruppi. Se le probabilità di sopravvivenza iniziali sono sensibilmente diverse tra i vari gruppi, è quasi certo che sopravviveranno alla fine solo individui del gruppo più favorito. E' bene verificare tutto ciò ripetendo più volte l'esperimento e variando ogni volta le probabilità di sopravvivenza.

 11 - Il problema dell'estinzione.
Un individuo di una certa specie vivente (ma anche una particella dell'atomo in un processo di fissione) può generare altri individui, ma può anche non riprodursi per niente. Supponiamo di conoscere le probabilità p₀ p₁ p₂ di generare 0, 1 o 2 discendenti. Qual è la probabilità che in un futuro più o meno prossimo si arrivi all'estinzione della discendenza?
Il problema è piuttosto complesso. Fu Galton a trovarne la soluzione. Se si suppone che un individuo possa generare al massimo due discendenti, l'equazione risolutiva sarà:

 12 - Sviluppo di popolazioni.
Il problema sembra semplice: qual è la probabilità che, dopo un certo numero g di generazioni, una popolazione, sviluppatasi a partire da un solo individuo, sia costituita esattamente da k individui? Per un numero un po' grande di generazioni il problema raggiunge un tale livello di complessità, da non consentire altra possibilità che quella di cercare di ottenere il dato richiesto per mezzo di prove ripetute.
I parametri da introdurre per la simulazione sono:

• p₀ p₁ p₂ probabilità di generare rispettivamente 0,1,2 figli.
• g numero di generazioni da considerare (consigliabile un numero non troppo grande)
• d numero di discendenti che si vogliono riscontrare alla g.ma generazione.

 13 - Guadagno di un giocatore.
Un giocatore ha una certa probabilità p di vincere ad un determinato gioco. Se effettua un gran numero di partite, potrà trovarsi in vincita, oppure in perdita (raramente, alla pari). Se la probabilità di vincita è pari a 1/2, i due eventi (vincita o perdita) potranno verificarsi indifferentemente. Ma se p è anche di poco superiore o inferiore a 1/2, allora andrà incontro rispettivamente a grandi vincite o a grandi perdite. Esse saranno tanto più grandi, quanto maggiore è il numero di partite giocate. Tutti i giochi d'azzardo danno al Banco un sia pur lieve vantaggio rispetto al giocatore. Questi è quindi destinato quasi certamente a perdere. La perdita sarà addirittura certa se deciderà di giocare un gran numero di partite. La durata del gioco dipenderà in ogni caso dall'importo del capitale iniziale, che potrà assicurargli un certo numero di partite, prima di trovarsi con le tasche vuote. Il programma è piuttosto semplice. Dopo aver introdotto il valore p della probabilità di vincita, s'inizia a giocare e sullo schermo appare il grafico del guadagno (o della perdita):
E' interessante fare più prove, assegnando inizialmente a p il valore 0,5. Si prova poi ad aumentare o a diminuire di poco la probabilità di vincita, ad esempio 0,52 e 0,48. Mentre nel primo caso il guadagno oscilla in genere intorno all'asse delle ascisse, negli altri due casi tenderà ad impennarsi rispettivamente verso l'alto (guadagno) e verso il basso (perdita).

 14 - Problema del collezionista.
Un bambino decide di fare una collezione di figurine. All'inizio tutte le figurine trovano posto nelle rispettive caselle dell'album. Ben presto però, il bambino scopre, nel sistemare le figurine, che alcune caselle dell'album risultano già occupate. Continuando a comprare figurine, capiteranno sempre più doppioni mentre le poche figurine mancanti sembreranno proprio non voler uscire.
Quante figurine dovrà acquistare in media ogni bimbo per completare il suo album? Il problema è stato già risolto. Per m caselle da riempire occorrono:
 

La formula è valida nel solo caso in cui le figurine siano messe nelle bustine in modo casuale. Valori troppo diversi farebbero supporre che il fabbricante abbia reso alcune figurine più rare di altre, per vendere una maggiore quantità di bustine. La simulazione dimostra che il trucco non è necessario. I bambini saranno costretti ad acquistare un bel numero di figurine, se vorranno completare la collezione. Proviamo a simulare una collezione, da ripetere per n volte, e vediamo quale valore medio si otterrà. Il risultato sarà, come al solito, vicino al dato teorico, se si sceglierà di fare molte prove. Si potrà sottolineare che la formula risolutiva non è molto facile da scoprire e che il metodo Monte Carlo, oltre che fornirci un risultato statistico, ci permette di valutare il grado di attendibilità di eventuali soluzioni proposte.

 15 - Il problema delle concordanze.
Supponiamo di avere un pacchetto di m cartellini numerati su una delle facce. Disponiamoli con la faccia nascosta e mescoliamoli accuratamente. Poi li scopriamo uno la volta, mentre contemporaneamente contiamo ad alta voce:

Tale risultato è sorprendente. Chi avrebbe mai pensato che dietro un giochetto con i cartellini numerati si celasse uno dei più noti numeri irrazionali? Per convincersi che non si tratta del frutto della mera fantasia di qualche matematico, non resta che cercare conferma con un buon numero di prove.

 16 - Il gioco del Craps.
Il Craps è un gioco di dadi abbastanza diffuso. Le regole sono un po' complesse.

• C'è un primo lancio di due dadi, durante il quale il Giocatore vince se esce il 7 oppure l'11 e perde se esce il 2 o il 3 o il 12;
• Se non vince né il Giocatore né il Banco, allora il numero uscito viene detto Punto e il gioco continua.
• Il Giocatore vince, se esce il Punto e perde, se esce il 7.

 17 - I cerini di Banach.

Successe proprio al matematico Banach di riflettere su una situazione derivata dalla sua abitudine di portare sempre con sé due scatole di cerini. Quando aveva bisogno di un cerino, lo prendeva da una delle scatole. Capitava, ad un certo momento, che la scatola da lui scelta si rivelava vuota. Era perciò costretto a prendere il cerino dalla seconda scatola se, fortunatamente, ne conteneva ancora qualcuno. Ecco nato il problema: quanti cerini restano in una delle scatole, quando l'altra viene trovata vuota (*)? La soluzione è piuttosto complessa e si conosce attualmente una formula che fornisce un valore leggermente approssimato, per un numero c di cerini: (2c+1)/Ö (pc) -1

 (*) Attenzione, il problema cambia se si suppone di andare a contare i fiammiferi dell'altra scatola, subito dopo aver acceso l'ultimo fiammifero di una scatola. Nel nostro caso si suppone che la scatola vuota sia rimessa in tasca insieme all'altra e, solo quando si cercherà di cavare da essa ancora un fiammifero, ci si accorgerà che è vuota. La formula si riferisce a tale situazione.

 18 - Il gioco dell'un-due-tre.
Si tratta ancora di un gioco sulle coincidenze, sul quale si basa un solitario con le carte. Si prende un mazzo di 40 carte napoletane. Dopo averle ben mescolate si scoprono una la volta e contemporaneamente si conta:
 

Se non si verificano coincidenze tra la carta scoperta e il numero che viene detto, si guadagna un punto. Quanti punti si ottengono mediamente in n partite? Si tratta di un problema aperto, di cui non si conosce a tutt'oggi la risposta. Non resta quindi che affidarci al metodo Monte Carlo, facendo un congruo numero di simulazioni.
Questa volta non abbiamo un valore teorico della probabilità con il quale confrontare quello stimato mediante il metodo Monte Carlo. Il calcolo delle probabilità ci assicura che bastano circa 38500 prove, per avere un valore della frequenza relativa le cui prime due cifre decimali si possono ritenere esatte, con una probabilità del 95%.
Le nostre simulazioni, basate su 80.000 prove, forniscono un valore medio di circa un punto per ogni 130 partite. Partendo da tale valore, qualcuno potrebbe cercare di risolvere il problema, facilitato dal fatto di sapere in anticipo una possibile soluzione approssimata.

 19 - Distribuzione uniforme.
Finora abbiamo operato con fenomeni di tipo discreto, in cui i singoli elementi dell'insieme di eventi sono distinguibili l'uno dall'altro, come le biglie di un'urna, e in numero finito. Passiamo ora ad occuparci di eventi in cui lo spazio campione è costituito da numeri reali o coppie di numeri reali. Per i numeri reali, così come per i punti di una retta o di un piano, non è possibile contare gli elementi contenuti in un intervallo. La combinatoria, alla quale si fa spesso ricorso nel calcolo delle probabilità, non può esserci più d'aiuto. Occorre pertanto far uso di altri concetti e di altre tecniche di calcolo.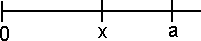
Esaminiamo una variabile uniforme nell'intervallo [0, a], che indicheremo con aR. R è un numero random compreso tra 0 ad 1, quindi il prodotto aR potrà assumere solo valori compresi tra 0 ed a. Se x è un numero compreso tra 0 ed a, la probabilità che un numero scelto a caso sia compreso nell'intervallo [0, x] è data dal rapporto x/a. Si può dare un'interpretazione geometrica (vedi figura a lato) al rapporto x/a: esso corrisponde al rapporto tra le lunghezze tra due segmenti, uno di lunghezza x ed uno di lunghezza a.
Scegliamo perciò due intervalli [0, a] e [0, x] con x < a e prendiamo a caso dei numeri nell'intervallo [0, a].
Qual è la probabilità che essi appartengano all'intervallo [0, x]? Come già detto, tale probabilità corrisponde al rapporto tra le lunghezze dei rispettivi segmenti. Il dato sarà facilmente confermato dalla simulazione.
Attenzione! Nel nostro caso stiamo supponendo che la probabilità che un punto a caso appartenga all'intervallo fissato non dipende da come viene scelto tale intervallo, ma solo dalla sua lunghezza rispetto a quella dell'intero segmento. In altre parole, la probabilità è distribuita in modo uniforme su tutta la lunghezza del segmento. Supponiamo invece che il punto a caso sia scelto da una goccia che si stacca a caso da un secchio che oscilla come un pendolo al di sopra delle due estremità del segmento. In tal caso la probabilità che una goccia cada all'interno di un certo intervallo dipende dal tempo che il secchio impiega ad attraversare lo spazio sovrastante. La velocità non è costante e quindi la probabilità non è distributa uniformemente lungo tutti i possibili intervalli.

 20 - Probabilità di (a £ R £ b) e di (c £ R £ d) in n estrazioni di R.

Se prendiamo due intervalli [a,b] e [c,d,] della stessa lunghezza all'interno dell'intervallo [0,1], la probabilità che un numero a caso appartenga all'intervallo [a,b] oppure che appartenga all'intervallo [c,d] è esattamente la stessa. Valgono, infatti, le considerazioni sulla distribuzione uniforme, fatte nell'esempio precedente.

Proviamo a verificarlo, con il computer. Per un numero di prove abbastanza grande le due frequenze relative tenderanno a coincidere.

 21 - Punti a caso in un quadrato unitario.

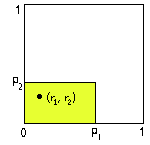Finora abbiamo scelto un numero a caso R. Ciò corrisponde, da un punto di vista geometrico a scegliere un punto a caso all'interno di un segmento di lunghezza a Proviamo ora a scegliere ora due numeri a caso, r1 e r2 nell'intervallo [0,1]. La coppia (r1, r2 individua un punto a caso all'interno di un quadrato unitario. Se ora fissiamo due numeri p1 e p2, ciascuno compreso nell'intervallo [0,1], la probabilità che il punto di coordinate (r1, r2) cada nel rettangolo di lati p1 e p2 risulta uguale al prodotto p1 p2, cioè all'area del rettangolo. Facciamo una simulazione, per verificare quanto è stato detto.

 22 - Area della superficie sotto la retta y=mx.

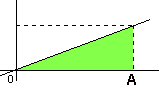
L'esempio precedente permette di affermare che la probabilità p che un punto appartenga ad una superficie piana S1 racchiusa all'interno di un'altra superficie piana S2 è data dal rapporto fra le corrispondenti aree. Viceversa, nota la probabilità p, possiamo affermare che l'area di S1 è uguale al prodotto di p per l'area di S2.

S₁ = p · S₂
Per un gran numero di prove, si può sostituire a p la frequenza relativa f/n.

 

S₁ = (f/n)·S₂
Su quest'ultima considerazione che si basa il metodo Monte Carlo per il calcolo di aree.

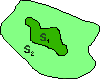
Per cominciare, consideriamo il caso molto semplice dell'area della superficie compresa tra la retta y=mx e l'asse delle ascisse, fino ad un punto A =(a,0) sull'asse delle ascisse. Il calcolo di tale area è molto facile: è la metà dell'area del rettangolo avente per base il segmento a che va dall'origine al punto A e per altezza l'ordinata ma della funzione, quindi è pari alla metà del prodotto a · ma, cioè:

ma²/2

L'area stimata con il metodo Monte Carlo, è molto vicina a quella calcolata geometricamente. Certamente, è facile trovare l'area del triangolo, anche senza ricorrere al metodo Monte Carlo. L'esempio è stato scelto solo per un primo approccio con la stima di aree per mezzo di metodi statistici.
Il metodo funziona ovviamente anche per stimare aree di funzioni più complesse, per le quali si richiede il calcolo integrale. Alcune funzioni non sono facilmente integrabili, perciò il calcolo delle loro aree potrebbe essere molto difficile, o in taluni casi addirittura impossibile. A questo punto è meglio una stima, sia pure un po' approssimata ... che nulla! La situazione è simile a quella che si ha quando occorre trovare il volume di un sasso. In mancanza di formule geometriche, si usa il rapporto tra peso e peso specifico. Si ottiene una misura che non è forse quella esatta, ma è comunque una sua buona approssimazione.

 23 - Un metodo statistico per il calcolo di p

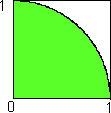Con centro in O e raggio 1 tracciamo un arco di circonferenza nel quadrato unitario. La probabilità P che un punto scelto a caso nel quadrato appartenga al settore è, come abbiamo visto, pari all'area del settore, cioè p /4. Moltiplicando per 4 si ottiene quindi p. Anche la frequenza relativa (numero di punti presi a caso e che appartengono al settore, diviso per il numero di prove ripetute), moltiplicata per 4, darà un valore approssimato di p.

Il programma fa apparire sullo schermo sia la figura sia i punti scelti a caso. L'uso della grafica rallenta alquanto l'esecuzione, anche se risulta di un certo effetto. Togliendo la grafica il programma diventa molto più veloce ed è possibile fare un maggior numero di prove in tempi accettabili, per migliorare l'approssimazione dei risultati.

 24 - Area sotto la parabola y=x².

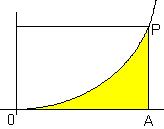Gli alunni di scuola media o del biennio delle superiori hanno sufficienti conoscenze di geometria, per calcolare direttamente l'area del triangolo sotto la retta o quella di un settore circolare di 90°. Se si passa invece ad aree di superfici più complesse, le loro conoscenze si rivelano insufficienti. Quando si ricorre al metodo statistico, non vi è invece alcuna differenza, dal punto di vista concettuale, tra l'area del triangolo sotto la retta e quella della superficie sotto la parabola o sotto l'iperbole.

Consideriamo ad esempio la parabola definita dalla funzione y=x²
Proviamo a trovare l'area delle superficie compresa tra la curva e l'asse delle ascisse, fino ad un punto A =(a,0), così come abbiamo fatto nell'esempio 22. Occorrerà tracciare un rettangolo che ha per base il segmento OA di lunghezza a e per altezza la misura a², corrispondente all'ordinata di P. L'area del rettangolo sarà data quindi dal prodotto a · a², cioè a³.
L'area della superficie sotto la parabola inscritta nel rettangolo è uguale al prodotto della probabilità p che un punto scelto a caso all'interno del rettangolo appartenga alla superficie sotto la parabola, moltiplicata per l'area del rettangolo. Sostituendo la probabilità con la frequenza relativa, si troverà, per un gran numero di prove, un valore approssimato dell'area. Per un gran numero di prove, la frequenza relativa, tende al valore 1/3. Perciò è facile arrivare a concludere che l'area della superficie sotto la parabola è 1/3 dell'area del rettangolo circoscritto.
Una volta ottenuta l'area sotto la parabola, si può trovare quella dentro il segmento parabolico, che si trova per differenza tra l'area del rettangolo ad esso circoscritto e quella della superficie sotto la parabola. Si ottiene così la formula per trovare l'area di un segmento parabolico, che è 2/3 dell'area del rettangolo circoscritto.

 25 - Area sotto l'iperbole y = 1/x

Occorre definire questa volta un intervallo [a,b] sull'asse delle ascisse, che individua una superficie sotto l'iperbole, nel tratto che va dal punto A=(a,0) al punto B=(b,0). Sappiamo, dal calcolo integrale, che l'area di tale superficie è pari a log(b)-log(a), cioè log(b/a).Se a=1, l'area diventa semplicemente log(b).

Tutto ciò ovviamente può essere presentato ad allievi che non sanno ancora nulla di calcolo integrale, facendo semplicemente uso del metodo statistico. Solo in seguito, avendo ottenuto una sufficiente dimestichezza con le aree delle superfici sotto l'iperbole, si potrà cogliere qualche interessante spunto per introdurre elementi non banali del calcolo dei logaritmi.
Per stimare l'area col metodo Monte Carlo, si traccia un rettangolo che ha per base il segmento lungo b-a sull'asse delle ascisse e per altezza l'ordinata (1/a) del punto P di ascissa a.
L'area del rettangolo sarà quindi: (b-a)/a
Tale area, moltiplicata per la frequenza relativa f/n dei punti che appartengono alla superficie sotto l'iperbole, rispetto al numero di prove, darà il valore approssimato delle relativa area .

 

BIBLIOGRAFIA
 

AA.VV.	Tre proposte didattiche per l'insegnamento di statistica e probabilità con l'utilizzo del computer	Progetto strategico C.N.R., tecnologie ed innovazioni didattiche per la matematica. Quaderno 5 (1990)
K.Baclawski, M.Cerasoli, G.C. Rota	Introduzione alla Probabilità.	U.M.I. Bologna (1984)
A.M. Cerasoli	La funzione RND nella simulazione di variabili aleatorie.	La matematica e la sua didattica (1988)
A.M. Cerasoli, M.Cerasoli	Elementi di calcolo delle probabilità	Zanichelli, 1987
M. Cerasoli	La Matematica dell'incerto	Insegnare, 5 (1986)
M. Cerasoli	Osservazioni sulla didattica della probabilità	La Matematica e la sua didattica (1988)
M.Cerasoli	Caso, probabilità e statistica visti dai grandi.	La Matematica e la sua Didattica, 2 (1994)
M. Cerasoli, G.Tomassetti	Elementi di Statistica	Zanichelli 1987
N.G. Cooper	From Cardinals to Chaos (Reflections on the Life and Lagacy of Stanislaw Ulam)	Cambridge University Press 1989
M. Cugiani	Metodi Monte Carlo e sequenze di numeri a caso.<	Periodico di Matematiche, XLV (1967)
I. Ekeland	A caso (La sorte, la scienza e il mondo).	Bollati Boringhieri (1992)
N.Metropolis, S.Ulam	The Monte Carlo method.	Journal of American Statistical Association 44(1949)
S.Ulam, R.D.Richtmyer, J.Von Neumann	Statistical methods in neutron diffusion	Los Alamos Scientific Laboratory report . LAMS - 551