|
Vittorio De Petris 1 - Il piccolo Gauss scopre la formula per calcolare la somma dei numeri da 1 ad n E’ noto l’episodio nel quale il giovanissimo e un po’ troppo vivace Gauss fu “punito” dal suo maestro che gli assegnò l’ingrato compito di calcolare la somma dei numeri interi consecutivi da 1 fino a 100. Erano passati pochissimi minuti, quando il piccolo Carl consegnò la risposta: 5050!
Moltiplicando 100 x 101 si ottiene 10100, che è il doppio della somma cercata. Non resta quindi che dividere per due, scrivere il risultato su un foglietto e consegnarlo all’allibito maestro. Il procedimento si può generalizzare, per calcolare la somma di numeri naturali da 1 ad n, che, abbinati nel modo in cui abbiamo visto fare da Gauss, formano n coppie. La somma dei due termini di ciascuna coppia è sempre (n+1).
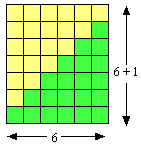
 2 - La versione geometrica Esiste anche una versione geometrica per arrivare alla suddetta formula.
3 - La media aritmetica. A questo punto della storia compiamo un salto fino ai nostri tempi, facendo entrare in scena la media aritmetica, molto usata nelle statistiche. Il calcolo è semplice: dato un insieme di valori, la
loro media aritmetica (Ma) è data dalla somma S dei valori, divisa per il numero dei termini (n):
 Si può pensare allora ad una formula inversa, in cui la somma dei termini è data dal prodotto della media per il numero di termini. In effetti la media si comporta come il famoso Robin Hood, che toglieva ai ricchi per donare a poveri: anziché avere tanti numeri diversi tra loro, la media ridistribuisce la somma in parti uguali, ottenendo n valori, tutti uguali alla media stessa. Supponiamo di avere un gruppo di 15 numeri: (4, 13, 1, 15, 8, 1, 21, 4, 8, 16, 14, 11, 19, 4, 8). La loro media è pari a 9,8. Possiamo immaginare di formare un nuovo gruppo, sempre di 15 numeri, tutti uguali a 9,8. La loro somma è semplicemente il prodotto di 9,8 x 15 = 147, cioè la media moltiplicata per il numero di termini. Qui casca l’asino, direbbe qualcuno. Se per calcolare la media si deve fare la somma e poi dividerla per n, allora la somma stessa è stata già calcolata e non serve calcolarla di nuovo! Giusto! Ma, se si riuscisse ad avere la media ... senza fare la somma? Consideriamo la successione dei numeri naturali d 1 ad n. Nel caso che n sia dispari, la media è data dal valore centrale della successione, come nelle dita di una mano in cui il medio è il dito numero 3: la somma dei primi 5 numeri è quindi pari al prodotto 3 x 5= 15.
Possiamo fare altri esempi e, ad un occhio ben allenato, non sfuggirà una regola elementare: la media dei primi n numeri naturali è sempre data dalla metà del successore di n, pari o dispari che sia n :
 Sostituendo tale valore nella (3), si avrà:
 Abbiamo di nuovo ottenuto per altra via la formula scoperta da Gauss. Altre strade possono condurre allo stesso risultato. Nulla di strano! In matematica tale circostanza è abbastanza frequente. L’importante è percorrere tutte le strade e magari scoprirne di nuove, per mantenere elastica la mente. 4 - La somma di numeri naturali compresi tra a e b. La media aritmetica può essere utilizzata anche nel caso in cui si voglia calcolare la somma di una successione di numeri naturali consecutivi compresi tra a e b. Basta calcolare i seguenti due valori: 1) La media aritmetica, che in questo caso è pari alla semi-somma dei due estremi: (a + b)/2
Come abbiamo visto in precedenza, la somma dei termini è data dal prodotto della media per il numero di termini: Esempio. Calcolare la somma dei numeri naturali da 15 a 70. La media è (15+70)/2 = 42,5. Il numero di termini è 70-15+1= 56.
E' evidente che, ponendo a = 1 e b = n, dalla (4) si ottiene di nuovo nella formula di Gauss, che quindi costituisce semplicemente un caso particolare della (4) stessa. 5 - La somma di numeri interi compresi tra a e b. Il procedimento appena descritto è valido anche nell'insieme dei numeri interi, costituito dai numeri naturali positivi, negativi e dallo zero. Si voglia ad esempio calcolare la somma di tutti gli interi compresi tra -7 e +15: la loro media, in base alla formula precedente, è (-7 +15)/2 = 4; analogamente, il numero di termini (zero incluso) è [(15-(-7)+1] = 23. La somma cercata è data quindi dal prodotto 4 x 23 = 92. 6 - La somma di numeri pari e dispari. Se abbiamo una serie di numeri pari da 2 a 2n, si può pensare di dividerli tutti per 2. Si avrà così una serie di numeri naturali da 1 a n, che sappiano essere uguale a n(n+1)2. Il risultato finale dovrà poi essere moltiplicato per 2. Resterà quindi il solo prodotto n(n+1). Ad esempio, la serie di numeri pari da 2 a 40, divisa per 2, corrisponderà al doppio di quella dei numeri naturali da 1 a 20, cioè 20 x 21. Generalizzando, la somma di numeri pari da 2 a 2n è uguale a n(n+1), cioè la metà del termine massimo moltiplicata per il suo successivo. Se abbiamo una serie di numeri dispari da 1 a 2n+1, applicando il criterio della media, visto al §3, dovremo:
Ecco dunque spiegato in modo analitico il fatto che la somma dei primi n numeri dipari da 1 a 2n + 1 è uguale al quadrato del numero di termini, soluzione già nota agli antichi greci che stavano studiando i cosiddetti "numeri quadrati", che servirono in seguito a costruire con un processo inverso l'algoritmo per calcolare la radice quadrata, tuttora insegnato nelle scuole medie. 7 - La Combinatoria. Osservando con un po' più di attenzione la formula di Gauss, ho notato una certa familiarità con una formula che si incontra in un contesto che non sembrerebbe avere nulla a che fare con la somma di numeri naturali. E' il caso delle Combinazioni con ripetizione, di cui si parla in un altro mio lavoro, disponibile su questo stesso sito: La combinatoria nella scuola media. Riassumiamo le principali caratteristiche di questo tipo di combinazioni: si ha un insieme di n elementi, diversi tra loro, ad esempio un gruppo di lettere dell'alfabeto, con cui formiamo varie combinazioni (parole) di k elementi, dove ciascun elemento può essere presente anche più di una volta. Non importa l'ordine con cui sono presenti le varie lettere, ma solo la loro quantità1. Nonostante la comune nozione di combinazioni, in cui la parola AABBB è considerata diversa dalla parola ABABB, in combinatoria le due parole sono equivalenti, essendo formate entrambe da due A e tre B, sia pure in ordine diverso. Per calcolare quante diverse combinazioni con ripetizione si possono ottenere con n elementi di classe k, si calcola il fattoriale crescente di k fattori a partire da n diviso per k! (k fattoriale):
 Ad esempio, con le 5 lettere ABCDE, prese a tre a tre, dovremo trovare tre fattoriali crescenti a partire da 5 e dividere per 3!. Avremo:  Cioè = 35 parole diverse di tre lettere, anche ripetute più volte all'interno di una parola. Poniamo il seguente quesito: quante combinazioni con ripetizione si possono formare con n elementi presi a due a due? Occorre calcolare il fattoriale crescente di 2 elementi a partire da n, cioè n(n + 1). Calcoliamo anche il fattoriale di 2, che vale semplicemente 2. Applicando tali risultati alla formula precedente, avremo:
 Anche la combinatoria è riuscita ad ottenere la formula di Gauss! Prima di pensare ad una mera coincidenza tra due situazioni così diverse tra loro (combinatoria e somma di numeri naturali), è bene andare alla ricerca di una possibile spiegazione. La risposta si ottiene osservando il modo con cui si formano le varie coppie di elementi che danno luogo alle diverse combinazioni. Partiamo da un insieme non troppo numeroso, ad esempio le lettere A B C D E F G. La lettera A può essere associata a sé stessa e a ciascuna della altre sei lettere, dando luogo alle seguenti 7 combinazioni: AA AB AC AD AE AF AG La lettera B non può essere associata alla A, poiché le combinazioni AB e BA sono equivalenti (l'ordine non ha importanza). Le ulteriori possibili combinazioni costituite con la lettera B sono quindi solo 6: BB BC BD BE BF BG Con la lettera C, non potendola associare né alla A né alla B, per le ragioni già indicate, le combinazioni si riducono a 5: CC CD CE CF CG. Analogamente, per le restanti lettere si hanno rispettivamente le seguenti combinazioni: DD DE DF DG (4 combinazioni)
Il numero complessivo di combinazioni con ripetizione dei nostri 7 elementi, presi a due a due, si ottiene sommando 7 + 6 + 5 + 4 + 3 + 2 + 1, cioè i primi 7 numeri naturali. Estendendo il discorso a quelle di n elementi, il loro numero equivale alla somma dei primi n numeri naturali.
|