Le idee di base dell'Analisi Matematica
Giulio C. Barozzi
Università di Bologna.

0. Premessa

Il corpo di dottrina che oggi chiamiamo Analisi Matematica ha ricevuto questo nome in epoca relativamente recente, anche se le idee di base affondano le proprie radici nella matematica greca classica. Il grande matematico svizzero Leonhard Euler (latinizzato Eulero) intitolava il suo più importante trattato Introductio in Analysim Infinitorum, pubblicato nel 1748. In esso si tentava una sistemazione delle conoscenze acquisite fino all'epoca della redazione dell'opera stessa, sulla base dei risultati di G.W. Leibniz e I. Newton, che a loro volta avevano sfruttato acquisizioni di B. Cavalieri, E. Torricelli, I. Barrow, e così a ritroso, fino ai grandi nomi dell'antichità greca, primo tra tutti Archimede.
Quali sono i problemi di base di cui si occupa l'Analisi Matematica? Dovendo operare una sintesi drastica (potrei dire: brutale) tali problemi sono riducibili a due: quello di determinare la tangente ad una curva data, grafico di un'assegnata funzione, e quello di determinare l'area sottesa dal grafico di una tale funzione.
Stabilire la connessione tra questi due problemi di base ha costituito un risultato di primaria importanza: non a caso tale connessione è, per antonomasia, il teorema fondamentale del Calcolo.

 1. La quadratura del segmento di parabola

Archimede (287-212 a.C.) si pose il problema di "quadrare" un segmento parabolico, cioè la regione mistilinea delimitata da una corda che congiunge due punti di una parabola e l'arco di parabola avente gli stessi estremi. L'idea di base è quella di invadere progressivamente il segmento parabolico mediante poligoni di cui si sa valutare l'area: si viene a costruire una successione s1, s2,...sn di aree che è crescente:

s1 < s2 < ... < sn <... ;

l'area del segmento parabolico sarà il più piccolo numero che non è superato da alcuna delle aree sn.
Incontriamo qui uno dei concetti di base dell'Analisi Matematica: quello di estremo superiore di un insieme di numeri reali: tra i numeri sn che costruiremo tra poco, non ce n'è uno che sia maggiore di tutti gli altri, perché ogni termine della successione è strettamente inferiore al termine seguente. A noi interessa il numero A che gode di queste due proprietà:
  1. ogni termine della successione sn non supera A: sn £ A per ogni indice n;
  2. A è il più piccolo numero che goda della proprietà 1), cioè se si considera un numero del tipo A - e , dove con e indichiamo un qualsivoglia numero positivo, allora per un certo indice n(e ) si ha sn(e ) > A-e

Vediamo la costruzione di Archimede, aiutandoci con un poco di Geometria Analitica. Consideriamo la parabola di equazione
y = p(x): = ax2 + bx + c,       a> 0,

e siano x1 e x2 due punti sull'asse delle ascisse con x1 < x2; consideriamo i punti P1 e P2 sulla parabola, aventi ascisse x1 e x2 rispettivamente, e finalmente conduciamo la secante passante per tali punti.

 


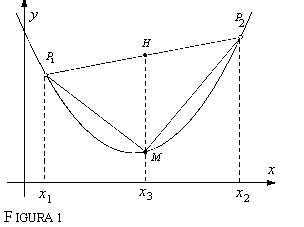La regione di piano di cui vogliamo definire e calcolare l'area è quella delimitata dall'arco di parabola costituito dai punti con ascissa compresa tra x1 e x2 e il segmento congiungente i punti P1 e P2.
Con riferimento alla figura 1, consideriamo il punto medio dell'intervallo [x1 , x2]:

e chiamiamo M il corrispondente punto sulla parabola: M := (x3, p(x3 ))
Una prima approssimazione (per difetto) dell'area che vogliamo definire, e al tempo stesso calcolare, sarà l'area del triangolo P1 P2 M: poiché il lato P1P2 ha come proiezione sull'asse x un segmento di lunghezza d :=x2-x1,
L'area di tale triangolo sarà dove H è il punto medio del segmento [P1 P2], dunque il punto di tale segmento avente ascissa x3.
Calcoliamo la lunghezza del segmento MH, sia h. Si ha, in base a semplici considerazioni di tipo geometrico,
h:= MH = (ordinata di H) - (ordinata di M) =

Dunque

 

(1)

A parole:
  • L'area del triangolo inscritto nel segmento parabolico delimitato dal segmento [P1 P2] ed avente come terzo vertice il punto M che ha come ascissa la semisomma delle ascisse di P1 e P2, è dato da 1/8 del prodotto del coefficiente a per il cubo della differenza d =x2 -x1 tra le ascisse dei punti P1 e P2.

Una prima conseguenza interessante: fissata una parabola, il coefficiente a è fissato; dunque l'area del triangolo inscritto nel segmento parabolico dipende solo da d, lunghezza della proiezione del segmento stesso sull'asse delle ascisse.
In altri termini: data una parabola, due triangoli inscritti in segmenti parabolici a cui corrispondano proiezioni uguali delle due corde sull'asse delle ascisse hanno uguale area, sempre che il terzo vertice abbia come ascissa la semisomma delle ascisse dei due restanti vertici.

 


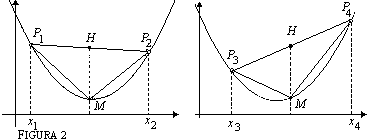Abbiamo così costruito un prima stima dell'area A:
s1 := A1

Una migliore approssimazione dell'area del segmento parabolico si ottiene sommando ad A1 le aree dei due triangoli P1MM1 e P2MM2, costruiti sulle corde P1M e MP2 esattamente come abbiamo fatto in precedenza sulla corda P1 P2 In virtù della formula (1), ciascuno di questi due triangoli avrà area

 


dunque la somma delle aree di tali triangoli varrà

 

A2 = 1/4 A1.

In definitiva la seconda approssimazione dell'area del segmento parabolico è

 


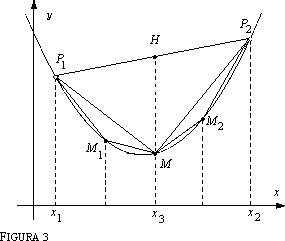
S2 := A1 +A2 = A1 + 1/4A1= A1 (1 +1/4).

Evidentemente si può proseguire allo stesso modo, raddoppiando ad ogni iterazione il numero dei triangoli inscritti nel segmento parabolico che si aggiungono ai precedenti: dopo n iterazioni, abbiamo per l'area A del segmento parabolico la stima per difetto:

 


A questo punto siamo tentati di dire che l'area A del segmento parabolico è il prodotto di A1 per la somma dei termini entro parentesi tonde, se invece di prenderne un numero finito, sia esso n, ne prendiamo infiniti. La cosa è vera, ma bisogna intendersi sul significato dell'espressione "somma di infiniti termini". Siamo di nuovo di fronte al concetto di estremo superiore: la somma degli infiniti termini

 


è, per definizione, il più piccolo numero che non è superato da alcuna delle somme

 

     (2)

Si tratta si sommare la cosiddetta serie geometrica, cioè di trovare il più piccolo numero che non è superato dalle somme di n + 1 termini in progressione geometrica, come sono appunto le somme (2).
Vediamo di calcolare questa somma, prima in termini intuitivi, cioè geometrici, poi in modo più rigoroso, con gli strumenti dell'Algebra. Il fatto che nelle somme (2) la ragione (cioè il rapporto costante tra un termine e il termine precedente) sia 1/4 non ha alcuna rilevanza particolare. Consideriamo, più in generale, una somma di termini del tipo
1 + r + r2 + r3 + ... + rn , (3)

con la condizione che sia 0 < r < 1. La quantità r è la ragione (dal latino ratio = rapporto). Costruiamo un triangolo rettangolo isoscele di lato 1, come mostrato in figura, e, sul prolungamento del cateto orizzontale, costruiamo un altro triangolo simile con i cateti lunghi r.

 


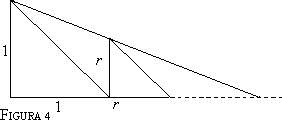Congiungiamo ora i due vertici dei triangoli appena costruiti con una semiretta, a partire dal vertice del triangolo di cateti uguali ad 1, fino ad incontrare la semiretta ottenuta prolungando il cateto orizzontale del medesimo triangolo (v. figura 4).

 


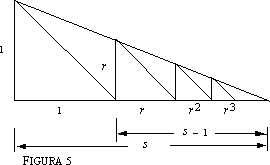Ora continuiamo a costruire triangoli rettangoli isosceli, uno a fianco dell'altro, in modo che i cateti orizzontali siano sempre sulla stessa semiretta, e i vertici che sono gli estremi dei cateti verticali siano tutti allineati con i vertici analoghi dei due primi triangoli.
Considerazioni semplici sulla similitudine dei triangoli ci dicono che i cateti di questi triangoli rettangoli isosceli sono in progressione geometrica di ragione T, dunque valgono successivamente T2, r3, T4,.
Se immaginiamo di poter proseguire indefinitamente questo procedimento, intuitivamente siamo condotti a dire che la somma di tutti i cateti orizzontali è uguale al cateto orizzontale del triangolo rettangolo che contiene tutti i triangoli costruiti.
La lunghezza di tale cateto orizzontale si calcola facilmente in base alla similitudine tra i triangoli in figura 5. Si ha
s : 1 = (s-1) : r Û sr = s-1 Û 1=s - sr = s(1-r),

da cui finalmente:

 


Allo stesso risultato possiamo arrivare se ricordiamo che la somma di n+ 1 termini in progressione geometrica, di primo elemento 1 e ragione r, si scrive

 


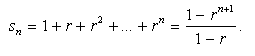Se nell'ultima frazione trascuriamo l'addendo rn+1 otteniamo la quantità 1/(1-r) che dunque è maggiore di tutte le somme sn . D'altra parte tale quantità è il minimo numero che non è superato da alcuna somma sn ; basta considerare che, essendo 0 < r < 1, le potenze rn si possono rendere piccole quanto si vuole, a patto di prendere n convenientemente grande.
Tornando al nostro caso: la progressione geometrica ha ragione r = 1/4. Dunque il più piccolo numero che non è superato dalle aree sn dei poligoni che abbiamo inscritto nel segmento parabolico è

 


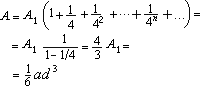Fino a questo punto abbiamo supposto che sia a > 0, cioè la parabola rivolga la propria concavità verso l'alto; il risultato ottenuto sussiste anche se a <0 (la parabola rivolge la propria concavità verso il basso): basta scrivere |a| al posto di a:

 


Teniamo presente che, se a > 0, allora il valore assoluto di a è l'opposto di a: |a|= -a. Verso la fine del nostro viaggio considereremo una parabola con il coefficiente a < 0.

 2. La tangente al grafico di una funzione: la derivata

Il secondo problema di cui dobbiamo occuparci è quello del tracciamento della tangente al grafico cartesiano di un'assegnata funzione y = f(x). Supponiamo di tracciare questo grafico rispetto un sistema monometrico ortogonale (niente paura: significa solo che gli assi sono tra loro perpendicolari e che si sceglie la stessa unità di misura sui due assi). Se (x0, f(x0)) sono le coordinate di un punto P0 che appartiene al grafico di f, sappiamo che tutte le rette passanti per P0 (con l'esclusione della parallela all'asse delle ordinate), sono date dalla formula

y = y0 + m(x - x0); (5)

il numero che ci interessa è m, il coefficiente angolare o pendenza della retta: esso ci indica di quanto varia l'ordinata di un punto sulla retta quando l'ascissa viene aumentata di un'unità.

 


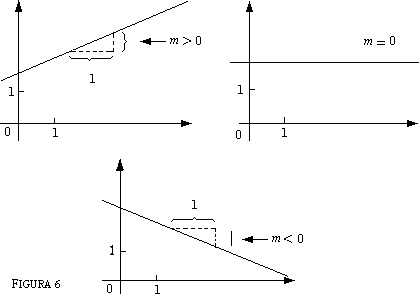Noi vogliamo determinare m in modo tale che la retta rappresentata dalla (5) sia tangente al grafico di f; questo particolare valore di m si chiama derivata della funzione f calcolata nel punto x0 e si indica con il simbolo f'(x0).
Per rispondere al quesito che ci siamo posti occorre riflettere sul concetto di tangente ad una curva. Supponiamo ancora che la nostra curva sia una parabola, quella di equazione y = f(x) = x2. Preso un punto x0, il corrispondente valore y0 vale x02; scegliamo sulla nostra parabola anche un secondo punto P di coordinate generiche (x, y) = (x, x2). Andiamo a scrivere l'equazione della secante che passa per P0 e P; il coefficiente angolare di tale secante è dato dal rapporto

 


Questo rapporto, fissato P0, dipende da P e dunque è anch'esso funzione di x. Trattandosi di un rapporto, chiamiamolo r(x):

 


Dato che la tangente è la posizione limite che la secante assume quando il punto P viene portato a coincidere con P0, la prima idea che viene è che, per calcolare il coefficiente angolare della tangente, basta prendere il coefficiente angolare della secante e vedere che cosa accade quando nella sua espressione si pone x = x0. Il guaio è che non succede proprio niente, perché, per x = x0, l'espressione del rapporto r(x) si riduce ad una scrittura del tipo 0/0, che non ha alcun significato.

 


Detto in altri termini: il dominio (o insieme di definizione) della funzione r non contiene il punto x0, anche se contiene tutti i punti distinti da esso. E' dunque possibile calcolare la funzione r(x) in corrispondenza di valori arbitrariamente prossimi a x0, ma non è possibile calcolarla in x0 stesso.
La situazione sembra disperata, se non fosse che un po' di algebra elementare viene in nostro aiuto. Vediamo se è possibile trovare un espressione equivalente al secondo membro della (6) per x ¹ x0, ma un'espressione che abbia senso anche per x = x0; il valore di tale espressione per x = x0 potrebbe essere quello che noi cerchiamo.
Ora non c'è bisogno di sapere molta matematica per ricordare il prodotto notevole x2 - x02 = (x - x0)(x + x0); dunque la (6) si scrive anche

 

     (6')

L'ultima espressione è definita anche per x = x0: essa vale 2x0.
Vediamo se questo è il valore giusto: quanto più x è prossimo a x0 tanto più r(x) = x + x0 è prossimo a 2x0. Qui siamo di fronte ad un altro concetto base dell'Analisi: il concetto di limite di una funzione.
Dire che una funzione f(x) tende ad un certo limite L quando x tende ad un valore x0 non vuole dire che f(x0) = L (anche se non si esclude che ciò possa accadere); vuol dire che f(x) si può rendere arbitrariamente prossimo a L a patto di prendere x convenientemente prossimo a x0.
Per tradurre tutto ciò in un procedimento verificabile, K. Weierstrass (1815-1897) ha introdotto la notazione e - d. Dire che il limite di f(x) per x che tende a
x0 vale L, significa che, comunque si fissi una tolleranza e > 0, si può determinare in corrispondenza una distanza d > 0 tale che, per gli x ¹ x0 appartenenti al dominio D della funzione, che distano da x0 meno di d si ha |f(x) -L|<e.

 


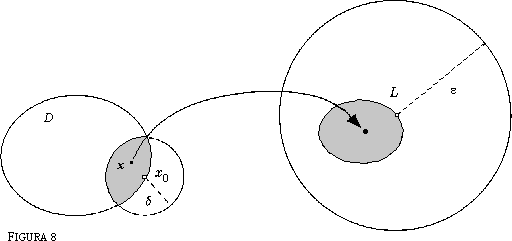Come dire: fissiamo un bersaglio centrato in L di raggio e > 0: se a partire da tutti gli x per cui 0 < |x - x0| < d i valori f(x) "colpiscono" il bersaglio, nel senso che |f(x) - L| < e , allora diciamo che il limite è L e scriviamo

Attenzione all'ordine con cui si scelgono le cose: prima si sceglie e (cioè il bersaglio), poi d (cioè il controllo); ci aspettiamo che, quanto più piccolo è il bersaglio, tanto più piccolo sarà il raggio dell'insieme di controllo.
Perché la definizione precedente abbia senso occorre che esistano x ¹ x0 in cui la f è definita, prossimi tanto quanto si vuole a x0 (in termini tecnici questo si esprime dicendo che x0 è punto di accumulazione del dominio di f), mentre l'eventuale valore della f nel punto x0 non influenza il limite della stessa funzione.
Torniamo al nostro rapporto r(x); poiché r(x)= x + x0, se vogliamo che sia
|r(x) - 2x0| =|x + x2 - 2x0| =|x - x0|<e

occorre e basta che sia |x - x0| < d =e , cioè basta prendere il raggio dell'insieme di controllo uguale al raggio del bersaglio.
In conclusione: se f(x) =x2, allora per ogni x0 reale si ha f'(x0) = 2x0. Dato che x0 è un qualunque numero reale, possiamo scrivere semplicemente x al posto di x0 e scrivere
f(x) = x2 Þ f'(x) =2x

Vediamo di ripetere il calcolo con una funzione un po' più difficile: f(x) = x3. Scriviamo il rapporto r che fornisce la pendenza di una secante passante per i punti di ascisse x0 e x; questo rapporto viene chiamato rapporto incrementale della funzione f. Nel nostro caso:

 


Se dividiamo x3 - x03 per x - x0 (ad esempio usando la regola di Ruffini), troviamo x2 + x0x + x02. Dunque

 


L'ultima espressione vale 3x02 per x = x0. Vediamo se riusciamo e verificare il test e - d di Weierstrass. Dobbiamo verificare che la differenza r(x) - 3x02 si può rendere in valore assoluto inferiore ad una qualsivoglia tolleranza prefissata, a patto di prendere x abbastanza vicino a x0. Ora si ha
r(x) - 3x02 = x2 + x0x + x02 - 3x02 = x2 + x0x - 2x02. (8)

Se x0 = 0, i giochi sono presto fatti: il secondo membro di (8) si riduce a x2 e si ha x2 <e se e solo se ; dunque
Supponiamo dunque x0 ¹ 0. Dalla (8) segue
r(x) - 3x02 = x2 + x0 x - 2x02 =
= x2 - x02 + x0x -x02 =
= ( x - x0 )( x + x0 ) + x0 (x - x0 ) =
= ( x - x0 )( x + 2x0 ).

Prendiamo i valori assoluti, e ricordiamo che il valore assoluto della somma non supera la somma dei valori assoluti:
|r(x) - 3x20| = |x - x0| | x + 2x0| £ |x - x0 | (|x| + 2|x0|).

A noi interessano i valori di x prossimi a x0, dunque non è restrittivo limitarsi a considerare gli x per cui |x|[2|x0|. Per questi x abbiamo
|r(x) - 3x02| [ 4|x0| |x-x0|

l'ultima quantità è minore di e per

 


In conclusione: d =e /(4|x0|).
Dunque tutto quadra: abbiamo

 


o anche, scrivendo semplicemente x al posto di x0,
f(x) = x3 Þ f'(x) = 3x2 (9)

La (7) e la (9) sono casi particolari di un risultato generale: per ogni naturale n³ 1, la derivata di f(x) = xn vale nxn-1. In formula:
f (x) = xn Þ f'(x) = nxn-1.

In generale la derivata di una funzione f è il limite del rapporto incrementale (sempre che tale limite esista):

 


Per procedere abbiamo bisogno di due teoremi sulle derivate: essi affermano che la derivata di cf(x) vale cf'(x), per ogni costante c, e che la derivata di f(x) + g(x) è f'(x) + g'(x).
A parole:
  • la derivata del prodotto di una costante per una funzione è uguale al prodotto della costante per la derivata della funzione; la derivata della somma di due funzioni è uguale alla somma delle rispettive derivate.
In formula:
(cf(x))' = cf'(x); (f(x) + g(x))' = f'(x) + g'(x).

Questi due risultati seguono dal fatto che i rapporti incrementali delle funzioni considerate si scrivono

 


e rispettivamente

 


Sarebbe bello se anche la derivata del prodotto di due funzioni fosse uguale al prodotto delle derivate: ciò è falso, ma dato che nel seguito non ci serve l'espressione della derivata del prodotto di due funzioni, tralasciamo questo argomento.

 3. Il teorema fondamentale del Calcolo

Fino a questo momento ci siamo occupati dei due problemi fondamentali dall'Analisi Matematica: quello di determinare la tangente ad una curva data, grafico di un'assegnata funzione, e quello di determinare l'area sottesa dal grafico di una tale funzione. A dire la verità, l'esempio con cui abbiamo esordito (calcolo dell'area di un segmento parabolico) non è esattamente quello che vogliamo.
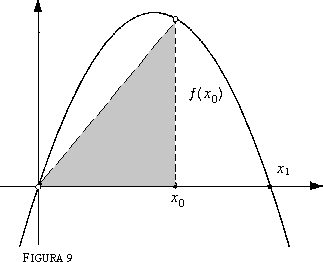Vediamo di riprendere in esame il problema. Consideriamo una parabola passante per l'origine del sistema di riferimento e rivolta verso il basso: la sua equazione sarà

y=f(x)=ax2+bx, a<0.

Tale parabola incontra l'asse delle x, oltre che nell'origine, nell'ulteriore punto x1 = -b/a. Supponiamo che b sia positivo, in modo che x1 sia anch'esso positivo, in quanto rapporto tra i numeri positivi b e -a. In figura 9 è rappresentata la parabola di equazione y = 2x2 +3x; tutto quello che diremo vale quali che siano i coefficienti a e b, purché siano negativo il primo, positivo il secondo.
Se vogliamo calcolare l'area del segmento parabolico individuato dall'asse delle ascisse, cioè quello che ha come corda il segmento che congiunge l'origine col punto (x1, 0 ), abbiamo la formula (4') pronta allo scopo: basta scrivere al posto di d il valore x1 = -b/a.
Questo problema è un po' troppo facile; vediamone uno più difficile. Scegliamo un valore qualunque xo compreso tra 0 e x1: 0 < x0 < x1; vogliamo trovare l'area della regione di piano che è delimitata dall'asse delle ascisse e dal grafico della funzione
f compreso nell'intervallo [0, x0), cioè la regione che è delimitata a destra dalla retta x = x0.
Esaminiamo la figura 9; la regione di cui vogliamo calcolare l'area è l'unione del segmento parabolico delimitato dalla corda che congiunge l'origine col punto (x0, f(x0)) e del triangolo di vertici l'origine e i punti (x0, 0) e (x0, f(x0)), ombreggiato in figura 9.
L'area di questo triangolo vale

 


Quanto all'area del segmento parabolico, abbiamo pronta la formula (4'); tale area vale

 


dove abbiamo tenuto conto del fatto che |a| = -a, a essendo negativo.
In conclusione l'area della regione che a noi interessa vale

 


Quest'area dipende dalla scelta di x0, cioè è una funzione di x0. Se scriviamo semplicemente x al posto di x0, abbiamo il seguente risultato: l'area compresa tra l'asse delle ascisse e la parabola in esame, relativamente alle ascisse comprese tra 0 e x, si scrive
A(x) := 1/3ax3+-1/2bx2. (9)

Abbiamo costruito una funzione della variabile x a partire dalla funzione f(x): è abbastanza naturale chiedersi se esista un legame tra queste due funzioni.
Proviamo a calcolare la derivata della funzione A(x): ricordando i due teoremi sulle derivate che abbiamo enunciato al termine del paragrafo precedente, abbiamo
A' (x) =1/3 a3x2+-1/2 b2x=ax2+bx.

Miracolo: abbiamo ritrovato la funzione f(x) da cui eravamo partiti:
A'(x) = f(x)

Sembra dunque che, data una funzione f, che possiamo supporre non negativa e definita su un intervallo [x0, x1], per costruire un'altra funzione che abbia come derivata proprio la f di partenza, basti procedere in questo modo: calcolare l'area della regione di piano compresa tra l'asse delle ascisse e il grafico della funzione f, relativamente ai punti le cui ascisse sono comprese tra x0 e x: si ottiene una funzione di x, sia A(x), che fa al caso nostro.
Naturalmente l'esempio precedente non prova proprio nulla, ma è, per così dire, un buon indizio.
In effetti i pionieri del calcolo infinitesimale, soprattutto E. Torricelli (1608-1647) e I. Barrow (1630-1677), che abbiamo citato all'inizio del nostro discorso, avevano intravisto, basandosi su esempi semplici proprio come abbiamo fatto noi, che i due problemi apparentemente così lontani, quello di calcolare l'area sotto il grafico di una funzione e quello di derivare una funzione (cioè trovare la pendenza di una tangente al grafico della stessa funzione) sono in realtà uno l'inverso dell'altro.
Il trucco è quello di pensare non ad un'area fissata, ma ad un'area che sia funzione del secondo estremo dell'intervallo [x0, x] su cui si proietta la regione che noi consideriamo.
L'operazione con cui si calcola l'area compresa tra l'asse delle ascisse e il grafico di una funzione va sotto il nome di integrazione, secondo una terminologia introdotta da G.W. Leibniz (1646-1716). Sempre limitandoci a considerare funzioni non negative, abbiamo che l'area della regione compresa tra l'asse delle ascisse, il grafico di f e le rette x = x0 e x = x1 si indica col simbolo

 


che si legge "integrale di f(x) in dx per x da x0 a x1". Il simbolo di integrale non è altro che una esse allungata, iniziale della parola latina summa, cioè somma. Leibniz, in ciò influenzato da B. Cavalieri (1598-1647), considerava la regione più volte considerata come "somma" di infinite striscioline parallele all'asse delle ordinate, ciascuna della quali ha una base "infinitesima" dx e l'altezza f(x).
Con i simboli introdotti da Leibniz e tuttora in uso, abbiamo

 


dove abbiamo usato una lettera diversa da x per indicare la variabile indipendente della funzione f per non confonderla con l'estremo superiore dell'intervallo su cui essa viene "integrata".

 


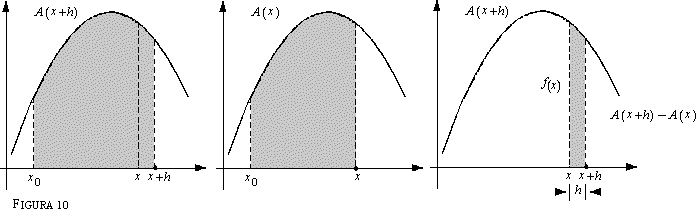Il teorema fondamentale del calcolo dice che per le funzioni f "abbastanza regolari" (ad esempio per tutte le funzioni elementari: polinomi, logaritmi, esponenziali, funzioni circolari ecc.) si ha che
A'(x) = f(x)

Un' idea della dimostrazione si ottiene se si scrive il rapporto incrementale della funzione A(x). Indichiamo con x e x + h i due punti in cui viene calcolata la funzione A e supponiamo, per semplicità, h > 0. Allora A(x + h) - A(x) rappresenta l'area sotto il grafico di f relativa all'intervallo [x, x + h], in quanto si tratta della differenza tra le aree relative agli intervalli [x0, x + h] e [x0, xJ (v. fig. 10).
Ne viene che per il rapporto incrementale della funzione A:

 


cioè il rapporto tra l'area relativa all'intervallo [x, x + h] e la "base" h della regione considerata. Se h è "molto piccolo" questa area non è troppo diversa dal prodotto h. f(x) (base per altezza), e quindi

 


Il ragionamento precedente, opportunamente "ripulito", diventa una vera dimostrazione.
Il cerchio è chiuso: se si integra una funzione su un intervallo che ha un estremo fisso e il secondo estremo variabile (chiamiamolo x) si ottiene una funzione che, derivata rispetto a tale estremo variabile, restituisce la funzione di partenza.