Mauro Cerasoli We analyze some parts of the mathematics born because the ruler and a pair of compasses exist. They turned obsolete after the advent of micro-computers, as TI-92. Recent ideas, subjects and themes of the modern mathematics, originated from these new instruments, are presented. Calcolare a manum est,
perseverare diabolicum! 1. Come è nata la matematica? La matematica creata dall'uomo dalla notte dei tempi fino al 1882, l'anno in cui Lindemann dimostrò la trascendenza di p, per fissare una data, ma anche molta matematica creata fino ai nostri giorni, è frutto dell'esistenza nella società umana di due strumenti molto semplici: la riga e il compasso.
Poiché prima o poi si porrà la questione dell'uso della calcolatrice simbolica e grafica in classe, per chiarirci le idee, vorrei subito replicare a chi la vieta adducendo la scusa seguente: lo studente deve imparare a fare i calcoli a mano perché altrimenti coma farà il giorno in cui non ha la calcolatrice? A parte il fatto che, il giorno in cui avrà un urgente bisogno pratico di calcolare un integrale, quasi certamente il nostro studente, divenuto oramai ingegnere, si troverà in un ufficio fornito di chi sa quanti computer di cui almeno uno perfettamente funzionante, c'è un'altra risposta di carattere concettuale. Intanto la scusa del collega contrario all'uso della calcolatrice contiene una ipotesi che ritroveremo in seguito, e che vorrei battezzare criptoipotesi, in attesa che qualche amico suggerisca un termine migliore. Nel dire che l'allievo deve saper fare i calcoli a mano si assume la criptoipotesi che si abbiano la penna e la carta! Questi però sono strumenti, senza dubbio più economici di un computer, ma sempre oggetti prodotti dall'uomo con tecnologia simile a quella necessaria per costruire un computer, che, guarda caso, potrebbero essere non disponibili nel giro di mille chilometri e di dieci anni! Ed allora come farà il nostro studente a svolgere i calcoli a mano? Inoltre non è possibile umanamente fare a mano certi conti. Si può trovare facilmente a mano il grafico della curva in coordinate parametriche x=cost, y=sent; meno facilmente quello della curva x=cos2t, y=sen3t, ma nessuno è in grado di trovare a mano quello della curva x=cos2t2, y=sen3t. Eppure abbiamo solo messo un 2 piccolo piccolo come esponente a t nella prima equazione della seconda curva! Misteri dell'algebra! Tuttavia basta TI-92 per vedere il grafico, un po' complicato, di questa curva di Lissajous modificata. Ma noi dobbiamo insegnare a far di conto, ribatte la giovane e bella maestra di Cantù, è quello che ci ripete ogni giorno la Direttrice. Allora alla Signora Direttrice raccontate questa scenetta di vita vissuta, eventualmente copiata da uno spot pubblicitario sull'uso di certe tecnologie intelligenti. Ad una delle casse del supermercato Coop di Bologna siede comodamente una bionda laureata in Matematica che, per mancanza di cattedre, ha preferito questo primo lavoro. Sorridendo, prende i vari pacchetti, bottiglie, scatolette ecc. del cliente e li passa sul banco elettronico creando una soneria di bip, bip. Ad ogni bip bip, sul monitor appaiono dei segni fosforescenti chiamati cifre: lei neppure li guarda. Alla fine dell'operazione, sempre sorridendo e tendendo la mano, si rivolge al cliente che nel frattempo ha estratto una tessera di plastica, a sezione aurea circa, chiamata Carta di Credito. La commessa gentilmente prende Carta di Credito e la fa passare attraverso la fessura di una macchinetta, lì a portata di mano. Avuto l'ok da mamma Banca, batte, senza pensare probabilmente al loro significato, i segni apparsi sul monitor della cassa e porge al cliente una pulsantiera. Vergognosetta, con un altro bel sorriso, gli dice: " digiti il suo codice segreto ", volgendosi con pudore dall'altra parte. Il cliente esegue l'operazione richiesta, si riprende la piccola Carta di Credito e il suo carrello, saluta e se ne va. E il far di conto? Abbiamo così quello che mi sembra il principio fondamentale che deve guidarci oggi nell'insegnamento della matematica: Iniziamo la nostra analisi elencando alcuni temi di matematica resi obsoleti per il semplice fatto che esiste una calcolatrice come TI-92 o programmi come Mathematica, Maple, Derive, Cabri Geometry ecc. 2. Un De profundis per il logaritmo? Le tavole numeriche, alla pari di riga e compasso, hanno fatto nascere una matematica che oggi è in via di estinzione. Non mi riferisco al fatto banale che nessuno cerca in quanto sia log2 che log 3 erano reperibili sulle tavole e l'ecc. si calcolava a mano. Oggi TI-92 mi dice subito che log41472 non solo è uguale a ciò che è scritto prima di ecc. ma che, numericamente, vale 2.36394. Morale della favola? Con la sparizione delle tavole si estigue la funzionalità del logaritmo a trasformare prodotti in somme. Per TI-92 calcolare ab equivale a calcolare a+b: non c'è alcuna differenza di tempo! Allora suoniamo le campane a morto per il logaritmo? Per quanto riguarda la funzione che aveva, si, ma per altre cose no. Come faremmo ad esprimere l'entropia senza il logaritmo? Nessuno sta pensando, spero, di riscrivere l'epitaffio sulla tomba di Boltzmann a Vienna. Ma come dice una bella canzone di Modugno: c'era una volta, or non c'è più. Pace all'anima del cologaritmo! Insieme a questo aspetto del logaritmo precipita agli inferi anche tutta quella matematica creata per applicare i logaritmi, cioè per trasformare somme in prodotti. Ad esempio, alcune formule di trigonometria, come le formule di prostaferesi e di Briggs. Visto che non abbiamo più bisogno dei logaritmi e che ci rimane del tempo perché i calcoli non si fanno più a mano, potremmo iniziare a parlare di quella matematica relativa al logaritmo che non sa TI-92. Mi riferisco alla sua proprietà di trasformare prodotti in somme (detta isomorfismo). Prendiamo ad esempio una progressione geometrica g0, g1,...,gn,... a termini positivi; ciò vuol dire che esiste un numero q , chiamato ragione (dal latino ratio ) tale che risulti In altre parole, il rapporto tra due termini successivi della progressione è uguale ad una costante q. Classico è il caso di q=1+i, dove i è il tasso d'interesse, un tasto a cui sono particolarmente sensibili i banchieri svizzeri (e non solo), e g0 è il capitale iniziale investito. Una progressione a0, a1,...,an,... è detta aritmetica se esiste un numero d tale che risulti an = an-1 + d. Che differenza passa tra una progressione geometrica ed una progressione aritmetica? Risposta: nessuna! Perché la progressione aritmetica an non è altro che la progressione geometrica gn trasformata con il logaritmo, ovvero ponendo an = loggn, d = logq. E questo TI-92 non lo sa, o almeno, se glielo chiedete non sa rispondere. Nel caso della capitalizzazione risulta d=log(1+i), con 0<i<1, e così possiamo capire perché lo sviluppo in serie del logaritmo è dato per la funzione y=log(1+x).
Infine, ritornando all'entropia, è bene ricordare che se X è una variabile aleatoria che assume n valori con probabilità rispettive p1,p2,...,pn allora la misura dell'informazione che essa dà su ciò che può accadere, cioè l'entropia, è data dalla formula 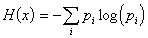 Oppure possiamo dire che il termine logaritmo non viene dalla fusione dell'espressione "numero della ragione" ma semplicemente dalla parola greca logariasmos. Termine trovato sulla ricevuta fiscale di un ristorante, e che dovrebbe significare in greco «ragionamento con i numeri», o più semplicemente conto. Infatti si dice spesso a qualcuno, per avvisarlo che sta facendo una cosa inutile, fare i conti senza l'oste. Pian piano dovrebbe iniziare ad affiorare così l'idea che da oggi la matematica si fa più parlando che scrivendo, più al bar, davanti ad una calda tazza di tè, come facevano Ulam, Banach, Steinhaus ed altri a Leopoli negli anni trenta quando ponevano le basi dell'analisi funzionale, della probabilità, della topologia ecc., che in un'aula sorda e grigia. 3. L'interpolazione fra punti Uno dei problemi classici e più antichi dell'analisi è stato quello dell'interpolazione. La tavoletta di argilla, classificata MLC2078 della Collezione Babilonese dell'Università di Yale, serviva a risolvere, mediante l'interpolazione, l'equazione
ossia a determinare il tempo x necessario per raddoppiare un capitale unitario, prestato al tasso di interesse i . Il problema particolare dell'interpolazione lineare viene usualmente espresso nel modo seguente. Si ha la funzione y=f(x) continua su un dato intervallo; per ipotesi sono noti i suoi valori f(a) ed f(b) in corrispondenza di due valori dati a e b. Si vuole determinare un valore approssimato di f(x*), corrispondente al dato x* , con a<x* < b. A tale scopo si considera la retta passante per i punti (a,f(a)) e (b,f(b)) che ha equazione Il valore approssimato di f(x*) si ottiene allora ponendo x* al posto di x nel secondo membro della relazione precedente. Da un punto di vista geometrico si approssima il valore della funzione con il valore della retta. Analizzando la questione un po' più a fondo vediamo che qualcosa non quadra dal punto di vista del buon senso. Intanto, se si dice «abbiamo la funzione f(x) e conosciamo i valori f(a) ed f(b)», qualcuno ci deve spiegare
Si potrebbe rispondere infatti brutalmente alla domanda posta dal problema dell'interpolazione: calcolati f(x*) così come hai calcolato gli altri due valori! Ma è qui che scatta la criptoipotesi: i due valori noti sono stati letti sulle tavole che riportano tabulata la funzione f(x), e sulle tavole il valore f(x*) non c'è! Ma allora abbiamo di fronte un problema di matematica generato, come si diceva all'inizio, dal fatto che esiste uno strumento fabbricato dall'uomo: un libro di carta stampata chiamato tavole numeriche. Che fine fa il problema e quindi la soluzione analitica quando davanti abbiamo TI-92 che per ogni x dello stesso tipo di prima, cioè in forma decimale e con otto cifre dopo la virgola, ci dà il valore esatto di f(x) fino alla cifra che vogliamo, e comunque ottimo per le applicazioni concrete? Quella del cologaritmo! Va nel cestino se non ci vengono dette altre sue pratiche applicazioni utili per la Confindustria, l'Associazione Commercianti, l'Unione Banche Svizzere, il Ministero della Difesa e chi più ne ha, ne metta. 4. Il calcolo di frazioni, radicali, integrali Una delle cose più antipatiche della matematica è il calcolo fine a sé stesso: senza alcun altro scopo. Effettuare una divisione come 209790:6426 è attività matematica tra le più aride e fredde che ci siano. Tanto è vero che adesso lasciamo questo compito al computer. Qualcuno potrebbe obiettare dicendo che fare quella divisione è più un compito del ragioniere che del matematico. D'accordo, ma allora perché nell'ora di matematica si fanno fare ai ragazzi esercizi di questo tenore su tanti altri simili argomenti? Lo studio delle frazioni, in particolare la semplificazione di frazioni, costituisce un primo esempio di calcolo inutile. Si chiede allo studente: semplifica la frazione a/b dove a e b sono due numeri naturali. Il problema nasce dal fatto che dovendo dividere a lire tra b persone conviene ridurre numeratore e denominatore in modo da semplificare la divisione finale. Così dividendo 209790 e 6426 per 2, per 9 e per 7, otteniamo 555 e 17: ora la divisione tra questi due numeri è più facile! Ma la faremo sempre con la calcolatrice! Anche perché questa divisione me la sono inventata, così da poter semplificare un po', mentre quelle vere, che si trovano nelle applicazioni, ad esempio 1234567891: 123456789, non si semplificano e ... vai subito con la calcolatrice! Infatti per TI-92 dividere 555 per 17 o 1234567891 per 123456789 è lo stesso lavoro. Così ci poniamo la domanda: fino a che punto sono utili le semplificazioni di frazioni? In particolare la scomposizione di naturali in fattori primi? Tra l'altro anche questo tipo di calcolo viene tranquillamente effettuato con il computer mediante il comando factor: è così che ho scoperto il fatto curioso che 1234567891 è primo.
Un discorso analogo vale per il calcolo di radicali e di integrali. Lasciamo perdere i radicali perché ormai solo colleghi scappati dal manicomio o che hanno avuto violenze da piccoli, e quindi bisognosi di vendicarsi a torturare i loro allievi, si ostinano a trattarli in classe più del minimo dovuto. Ma gli integrali non possiamo trascurarli: quelli servono! E giù a fare altri calcoli inutili dei più svariati tipi di integrali in tutte le salse. E così passano vari mesi per imparare a leggere, scrivere e far di conto. Ma che cosa è un calcolo di integrale? Esattamente come il calcolo della divisione precedente 209790:6426. Quando dividiamo a per b due sono i casi: o il loro rapporto è un numero naturale, oppure, semplificata, a/b è una frazione vera e propria, con tanto di numeratore e denominatore, equivalente a quella data. Analogamente accade per l'integrale 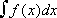 .Anche qui due sono i casi: o l'integrale esiste, ad esempio è uguale alla funzione F(x)+c, e quindi è una funzione come tutte le altre, così come 1998:3 è uguale al numero naturale 666 (oilà!, il numero della bestia, altro argomento interessante per fare matematica dilettevole), oppure non esiste l'integrale ed allora abbiamo una funzione integrale, cioè un vero e proprio integrale. Ad esempio nel caso di f(x)=exp(-x2), n cui nasce la nuova funzione .
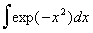Pertanto, invece di perdere tempo nel calcolare integrali inutili, perché non filosofiamo un po' su questo concetto e su quello di funzione? Ad esempio ad analizzare il fatto che in certi casi puoi cambiare il valore della funzione f(x) in infiniti punti dentro un intervallo senza che cambi il valore dell'integrale su quell'intervallo. Perché non proviamo a far vedere quali sono i campi di applicazione della matematica dove ciò che conta, ma non in senso aritmetico, più che la funzione è il suo integrale che spesso, per volere di Satana, non è calcolabile elementarmente, come la funzione integrale di Gauss? Perché non introduciamo subito la funzione gamma di Eulero con tutte le sue prorietà fattoriali? Potremmo studiare le proprietà formali della funzione logaritmo intesa come integrale di 1/x o di arcotangente e così via. Oppure far notare che molti teoremi di analisi furono prima scoperti per le funzioni polinomiali e poi per le altre, così da chiarire perché spesso appaiono i nomi di due matematici in un teorema. E così via. Tanto ormai l'integrale di 1/(1+x4) lo fa TI-92. 5. Discreto o continuo? Restando nel campo dell'analisi matematica scopriamo che la presenza del computer ha ridimensionato alcuni dei suoi strumenti principali, ad esempio la derivazione. Prendiamo lo studio di funzioni. Per disegnare il grafico di una funzione vengono impiegate prima o poi le derivate: servono per trovare i massimi e i minimi, i punti di flesso, la crescenza e decrescenza, la concavità. Anche in questo caso partiamo da una criptoipotesi: data la funzione y=f(x) non siamo in grado di tracciare il suo grafico per punti in quanto dovremmo eseguire un numero straordinariamente grande di calcoli. Se volessimo un tratto del grafico sull'intervallo [0,1], procedendo a passi di un decimo di millimetro, quando l'unità di misura è il decimetro, dovremmo calcolare un centinaio di valori di f(x). Un lavoro lungo e antipatico! Così applichiamo le derivate, troviamo i punti di massimo e di minimo, i flessi, la crescenza, la concavità e ...oplà, il gioco è fatto! Con pochi punti a disposizione tracciamo con la penna, in modo continuo, il grafico della funzione f(x). Ora è vera la criptoipotesi, non possiamo stare a calcolare cento o più punti a mano, conviene fare la derivata, ma dove sta scritto che l'equazione f'(x)=0 ha le soluzioni facili da trovare? Non è stato forse il docente, o il Ministero della Pubblica Istruzione, a scegliere la funzione f(x) in modo tale che f'(x)=0 sia un'equazione facile da risolvere a mano? Per intenderci, non del tipo f(x)=x2 cosx+e-x!
quando invece quasi tutti hanno studiato il loro limite per x ® 0 o per x ® ¥ ? Il computer, grazie a Dio, riporta il problema alla sua forma originale, cioè discreta. Ma il grafico di una funzione f(x) come viene definito? Non è l'insieme dei punti del piano cartesiano di coordinate (x,f(x)) al variare di x nel suo dominio? Vuoi disegnare il grafico? Cioè vuoi vederlo? Allora è come al cinema o nei cartoni animati o nella televisione: un insieme discreto di punti sufficienti per darti l'idea della curva e più in generale di una figura. E' ciò che fa il computer quando ti disegna la curva per punti con un sufficiente grado di precisione (in termini di pixel). Ma fin qui tutto bene perché le funzioni in questione erano supposte derivabili nei punti critici! E quando non lo sono invece, come come facciamo a trovare i massimi e i minimi? Vogliamo spiegare agli studenti l'algoritmo di Kiefer che utilizza i numeri di Fibonacci per risolvere questo problema? Altrimenti non resta che affidarci di nuovo a TI-92. Se qualcuno sta pensando all'utilità delle derivate nel calcolo di limiti di funzioni, cioè al teorema di De l'Hospital, fa ancora in tempo a rimangiarsi la gaffe. Se il collega insiste a salvare De l'Hospital, si sbrighi a presentare un esempio di applicazione utile del teorema suddetto, diversa dal calcolo di limiti inutili, appositamente resi complicati dal docente, ma facilmente calcolabili ad occhio con un uso intelligente dello sviluppo in serie di Taylor. L'alternativa è di fare una brutta figura con gli studenti che poi non sono così fessi come qualcuno va dicendo in giro. A proposito degli sviluppi in serie di Taylor: qual è oggi la loro importanza dal punto di vista numerico? Circa trenta anni fa uscirono le prime calcolatrici tascabili che effettuavano le quattro operazioni elementari. Fu naturale allora dire agli studenti che ci si poteva calcolare senx con quelle, quando x era piccolo, vicino allo 0, approssimandolo con il trinomio Era l'inizio della fine delle tavole numeriche, avvenuta qualche anno dopo quando apparvero le prime calcolatrici scientifiche. Ma con queste entrava in agonia anche la formula di Taylor perché a che cosa interessava più ormai visto che senx lo calcolavo, e lo calcolo, direttamente schiacciando un tasto? Era un altro duro colpo per le derivate e la loro brillante carriera nella storia della matematica? Anche qui, un altro modo di vedere le serie di potenze, già noto a Laplace fin dal 1795, cioè l'aspetto formale come funzione generatrice, salva la vita alla formula di Taylor. Scrive infatti il grande matematico francese: "Si l'on conçoit une fonction A, d'une variable t, développé dans une série ascendante par rapport aux puissances de cette variable, le coefficient de l'une quelconque de ces puissances sera une fonction de l'exposant ou indice de cette puissance. A est ce que je nomme fonction géneratrice de ce coefficient ou de la fonction de l'indice". Ad esempio, se c e t indicano semplicemente croce e testa allora il coefficiente di tk nella potenza del binomio (c+t)n indica in quanti modi possono uscire k teste ed n-k croci in n lanci di una moneta. E' il numero di parti di cardinalità k contenute in un insieme di n elementi. Analogamente, il coefficiente di tk nello sviluppo della serie (1-t)-n è il numero di multinsiemi (o insiemi con elementi ripetuti, combinazioni con ripetizione) di k elementi costruiti da un insieme di n elementi. E la convergenza? Grazie, ma in questo ambito non ne abbiamo bisogno. Stiamo utilizzando le serie formali! Non dobbiamo fare somme ma solo indicare il coefficiente di qualcuno nello sviluppo di qualche cosa. Ciò equivale a dire che non stiamo guardando la foresta dall'alto, come quando si va in aereo, bensì che ci stiamo passeggiando all'interno, osservando e ammirando i suoi alberi uno per uno! 6. Gli strumenti cambiano il modo di pensare? Allora lo strumento cambia il modo di vedere le cose? In questo caso l'uso formale delle serie era già noto, prima che arrivassero i computer, e quindi lo strumento ci dà solo più tempo da dedicare all'aspetto formale piuttosto che a quello numerico, dove si fanno veramente le somme e i prodotti. Ci sono altri esempi in cui la nascita di un particolare strumento può ridimensionare, se non addirittura demolire, un modo di pensare. Si è già visto nel campo sociale come la lavatrice dei panni e la lavastoviglie, per non parlare della cucina a gas, abbiano radicalmente cambiato la condizione femminile nelle civiltà industrializzate. In matematica prendiamo ad esempio la teoria degli errori. Essa è nata perché nel misurare certe grandezze fisiche si commettono errori. Se misuro la larghezza della mia scrivania 100 volte ottengo in genere 100 misure differenti, ad esempio, in metri
Applicando la teoria della stima, ricavo, sempre ipotizzando, l'intervallo di confidenza 1.761 ± .005. Possiamo dire che la mia scrivania è larga, più o meno, un metro, 76 centimetri ed un millimetro. Ora tutto questo è dovuto alla criptoipotesi che sto usando un metro da falegname, o della sarta, che apprezza il millimetro e così via. Ma che cosa succede quando per misurare utilizzo uno strumento elettronico che mi da queste altre 100 misure: cioè tutte misure in cui le prime sei cifre decimali sono sempre le stesse? Che posso prendere come stima di quella larghezza il valore 1.761432 esatto fino al millesimo di millimetro! Che fine ha fatto la teoria degli errori? Sopravvive, ovviamente, per mia fortuna, ma ora mi serve solo in quei casi in cui oggettivamente ho quelle 100 misure in genere tutte differenti. E' questo il caso in cui voglio misurare il colesterolo medio di un uomo di 50 anni: in genere 100 uomini campionati danno, all'analisi del sangue, 100 valori più o meno differenti, ed allora lì è necessaria la teoria degli errori. Ma in altri casi lo strumento ha ridato vita a teorie che sembravano destinate all'oblio dei secoli. Pensiamo per un attimo ai frattali o agli insiemi di Julia per fare un primo esempio. L'equazione z3=2 ha tre soluzioni nel campo complesso che chiameremo p1, p2, p3. Proviamo a cercarle utilizzando l'algoritmo di Newton-Fourier, cioè la ricorrenza, valida per risolvere appunto l'equazione f(z)=0. Nel nostro caso la ricorrenza diventa L'algoritmo inizia con un valore z0 scelto a piacere nel piano complesso. A seconda del punto z0 scelto si ottiene una delle tre soluzioni. Il piano viene così diviso in tre parti C1, C2, C3 formate nel modo seguente: per ogni i=1,2,3 l'insieme Ci è costituito dai valori iniziali z0 che portano alla soluzione pi. Questo fatto fu osservato per la prima volta da Cayley nel 1879. Come sono fatte queste parti? Per vederle è necessario simulare il tutto al computer. Infatti solo con il computer è stato possibile realizzare tali figure, chiamate poi frattali, ed oggi osservabili a colori su internet alla voce fractals. Così il computer ha ridato vita a quel ramo della geometriache era umanamente impossibile vedere a occhio nudo. Niente dinuovo sotto il sole: e' avvenuto un po' come per il cannocchialee per il microscopio nei confronti rispettivamente dell'astronomiae della biologia. I nuovi strumenti portano in soffitta certeteorie e ne fanno nascere altre: c'est la vie! Un altro esempio di teoria nata, come Minerva, dalla testa delcomputer, è il metodo Monte Carlo (vedi articolo su questo sito). Questo algoritmo ha senso, è realizzabile in pratica, solo con il computer. Se voglio sapere qual è la probabilità che riesca un certo solitario, complicato abbastanza da non poter essere calcolata teoricamente, mi affido alla sorte, gioco il solitario un numero elevato di volte, diciamo 10.000 volte, e poi stimo la probabilità teorica facendo il rapporto tra il numero di volte che mi è riuscito e 10.000. Un esempio potrebbe essere il solitario dell' 1-2-3. Dai le carte e le metti sul tavolo a tre a tre dicendo ogni volta 1, 2 e 3. Il solitario riesce se non esce mai un asso quando dici 1, un due quando dici 2 e un tre quando dici 3. Ma il metodo Monte Carlo non serve solo per giocare solitari, sappiamo infatti che i matematici si interessano solo di cose serie ed è per questo che se ne parla. Esso è utile per calcolare integrali o per risolvere problemi ancora più complicati. Può ripetere in breve tempo milioni di prove e farne le statistiche! Ma c'è di più, stando a quello che diceva Gaetano Fichera in una famosa conferenza tenuta il 13 marzo 1993 all'Accademia dei Lincei: Domani, quando per calcolare un'area sarà molto più rapido e conveniente usare un metodo Monte Carlo anziché, ad esempio, calcolare un integrale, la definizione di area sarà sempre quella di Peano-Jordan (o anche di Lebesgue) o non, piuttosto, quella che può darsi mediante un'interpretazione probabilistica del concetto di area? E pensare che questa idea, a proposito di lunghezza di una curva, partendo dal problema dell'ago di Buffon della metà del 700, era venuta al matematico francese Barbier nel 1860, quando ancora non esistevano i computer. Si può dimostrare infatti quanto segue. Una curva semplice C,di lunghezza finita l(C), topologicamente equivalente ad un segmento, viene lanciata a caso sul piano cartesiano. Sia Xil numero aleatorio di punti di intersezione che C ha con le rette di equazione y=k, essendo kÎZ.Sia <X> la speranza matematica, o media, della variabile aleatoria X. Allora vale la formula Il computer non fa solo calcoli, nonostante il nome, puòfare anche dimostrazioni di teoremi! Sono passati ormai piùdi venti anni da quando K.Appell e W.Haken provarono nel 1976 il teorema dei quattro colori utilizzando un computer e sollevando un vespaio di discussioni tra matematici e filosofi sul concetto di dimostrazione. Sempre con lo strumento elettronico, dopo un anno ininterrotto di lavoro, è stato dimostrato più recentemente che non esiste il piano affinedi ordine dieci. In pratica ciò significa che non èpossibile, dato un insieme di 100 elementi, detti punti,determinare 110 sue parti, dette rette, tali che
Entriamo così nel mondo della matematica discreta, o meglio finita, dove i concetti classici di spazio e tempo,come intendevano Zenone, Newton Minkowski ed Einstein non esistono. Se aggiungiamo un'altra parola mitica di questo secolo, caso, a quella di computer già troppo da noi usata, scopriamo quali sono i temi fondamentali che ci devono guidare nella ricerca e nella scelta della nuova matematica da insegnare. La probabilitàe la statistica non hanno bisogno di pubblicità per entrare a pieno titolo tra i nuovi contenuti dei corsi di matematica. Si dice spesso che l'insegnamento della matematica contribuisce a formare l'allievo forse più di qualunque altra materia. Ma che tipo di allievo vogliamo formare? Sentiamo cosa diceva della scuola nel 1995 il genetista Luca Cavalli Sforza:Che si tratti di un anziano senatore o di un giovane fanatico, il razzista è un tipo difficile da convincere. Credo che gran parte dei pregiudizi vengano trasmessi dalla famiglia edè per questo che la scuola può giocare un ruolo importante. Io farei studiare a tutti un po' di medicina e anche il calcolo delle probabilità, per aiutare a comprendere l'importanza del caso (vedi la fine del Titanic). Mauro Cerasoli, Fac. Scienze (Università del'Aquila) mauro.cerasoli@alice.it. Parte della relazione tenuta dall'Autore al corso "Quale matematica dopo la scuola dell'obbligo ?" Canobbio (CH),9-10 marzo 1998 |
o log7 o sen35° sulle tavole: siamo tutti d'accordo che basta digitare log7 per sapere quanto vale! Penso invece ad altro; per esempio, ai tempi del mio liceo classico, 1963, ricordo che log8 diventava sempre 3log2. La giustificazione era la seguente, per la criptoipotesi: esistono le tavole! Infatti poichè le tavole arrivavano fino a 1000, dovendo calcolare log41472 si scriveva
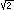e storia della scuola pitagorica e della colpa di Pitagora nella morte di Ippaso da Metaponto; 
| 
|
| 
| |