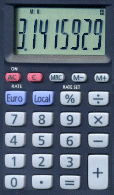Breve storia di un numero famoso: p
Dai babilonesi ... ai giorni nostri.
di Vittorio De Petris

Liberamente tratto da «Storia del Pensiero Matematico» di Morris Kline - Giulio Einaudi Editore 1991


Il nome di babilonesi viene dato ad una serie di popolazioni che, in tempi successivi, occuparono la Mesopotamia, una regione del Medio Oriente situata tra il Tigri e l'Eufrate. Tra di esse ricordiamo le popolazioni dei Sumeri, che per primi occuparono tale regione a partire dal 4000 a.C., seguiti dagli Akkadi (2200 a.C.), dagli Assiri (800 a.C.), dai Caldei (700 a.C.), dai Persiani (540 a.C.), fino alla conquista della Mesopotamia da parte di Alessandro Magno nel 330 a.C. Il massimo periodo di fioritura della cultura babilonese si ebbe tra il 2200 a.C. e il 1700 a.C.
In Mesopotamia il ruolo della geometria era insignificante e quasi sempre legato ad applicazioni pratiche. I babilonesi conoscevano certamente il teorema di Pitagora (o meglio alcune terne pitagoriche, senza porsi il problema di una loro generalizzazione ) e la similitudine dei triangoli. Per ottenere l'area del cerchio usavano la formula A=c2/12, dove c indica la circonferenza. Ciò equivale ad usare per p il valore 3. Ed è proprio da 3, come nel film di Troisi, che comincia dunque la nostra storia.
Per calcolare la lunghezza della circonferenza inscritta nell'esagono regolare, i babilonesi usavano un rapporto che implicava per p il valore di 3+1/8, che equivale a 3,125.
Il valore assegnato a p dai babilonesi era approssimato per difetto. Gli antichi egizi assegnavano invece a p un valore approssimato per eccesso. Essi calcolavano l'area del cerchio mediante la formula A=(8/9 d)2, dove d è il diametro. In questo caso p assume il valore 256/81 (circa 3,1605).
Occorre arrivare al grande Archimede di Siracusa (287-212 a.C.), per avere i primi due decimali esatti di p. Egli cerca di calcolare la lunghezza della circonferenza per mezzo del perimetro dei poligoni inscritti e circoscritti. La circonferenza ha infatti una lunghezza compresa tra il perimetro di un poligono inscritto e quello di un poligono circoscritto ad essa.
Le misure di tali perimetri si avvicinano sempre più tra loro con l'aumentare del numero dei loro lati, permettendo di restringere sempre più l'intervallo entro il quale dev'essere compresa la misura della circonferenza che si desidera trovare. Per tale via, egli riesce quindi a stabilire due valori tra cui p è compreso: (3+10/71) <p < (3+1/7). Il primo dei due valori vale 3,1408... e il secondo vale 3,1428...
Sono occorsi quasi due millenni per passare da una a tre cifre esatte del nostro numero. Non basterà invece il tempo passato e futuro dell'umanità per trovare tutte le altre cifre.

E' stato dimostrato infatti da Lambert nel 1761 che p è un numero irrazionale. Perciò le sue cifre decimali sono illimitate e non periodiche e nessuno potrà mai scriverle tutte. Successivamente, nel 1882, Lindemann dimostrò che p è un numero trascendente (significa che esso non può essere ottenuto da un'equazione algebrica a coefficienti razionali), ponendolo in una particolare categoria di numeri irrazionali, che si distinguono rispetto a quelli cosiddetti algebrici .
Pur non potendo quindi scrivere tutte le cifre di p, alcuni grandi matematici hanno tuttavia affrontato il problema di scoprire un procedimento che permettesse di trovare quante cifre decimali si desiderano.
Riprendiamo quindi il nostro racconto per descriverne le tappe più significative.

I romani, si sa, non dedicavano molti sforzi allo studio delle scienze (che non fossero quelle giuridiche o militari). Essi si limitarono alla conoscenza, senza ulteriori approfondimenti, delle opere dei greci. Gran parte della geometria di Archimede, per via della sua complessità, finì per essere dimenticata.
Gli uomini del medio evo dovevano risolvere problemi di stretta sopravvivenza (del corpo e dell'anima) e non potevano certo dedicarsi agli studi.
Dobbiamo perciò arrivare al Rinascimento, per assistere ad uno spettacolare rifiorire della scienza. In tale periodo, tra i matematici, si sviluppò un'ampia ricerca sui numeri irrazionali.
François Viète (1540-1603), riprendendo il metodo di Archimede ed usando le radici quadrate, calcolò il valore di p considerando poligoni regolari di 4, 8, 16,... lati inscritti in un cerchio di raggio unitario. Per tale via egli trovò che il valore di p è dato da:


Il reciproco del valore ottenuto, moltiplicato per 2, fornisce un valore sempre più approssimato di p, quanto maggiore è il numero di termini. I primi quattro termini forniscono il valore approssimato 3,140331 con le prime due cifre decimali esatte. Con sei termini si ha: 3,141513, le cui prime quattro cifre decimali sono esatte. Occorrono dieci termini per avere sei cifre decimali esatte: 3,141592...
L'inglese John Wallis, nella sua Arithmetica infinitorum (1655), usò una frazione, i cui termini sono costituiti da una serie ininterrotta di moltiplicazioni. Dal numero di fattori usati dipende l'approssimazione di p:

p/4 = (3.3.5.5.7.7...)/(2.4.4.6.6.8...)

Wallis usava numeri razionali per calcolare p, contrariamente a Viète che usava le radici quadrate. Tuttavia la formula di Wallis richiede almeno 1000 termini per avere le prime due cifre decimali esatte di p.
Il grande Gottfried Wilhelm von Leibniz ottenne nel 1674 il famoso risultato:


Siamo dunque arrivati a definire p come il quadruplo della somma a segni alternati dei reciproci nella successione dei numeri dispari. Peccato che occorrano ben 764 termini per calcolare p anche solo con la precisione ottenuta da Archimede.
A questo punto va detto che il nostro p non ha ancora assunto il suo attuale nome.
Fu il matematico inglese William Jones che, nel 1706 usò il simbolo p, in onore di Pitagora (l'iniziale di Pitagora nell'alfabeto greco è appunto P, ma, trattandosi di un numero, si preferisce usare la minuscola ). Tuttavia, ancora nel 1739 lo svizzero Leonhard Euler (1707-83), da noi italianizzato in Eulero, usava il simbolo p.
Fu proprio Euler nel 1743 a fornire una ennesima formula per il calcolo di p:


La formula di Euler è più efficace di quella di Leibniz, per il fatto di usare solo termini positivi. Essa richiede tuttavia un numero di termini ancora piuttosto alto per ottenere le prime due cifre decimali esatte di p. Per avere 3,14 occorrono almeno 600 termini, contro i 764 richiesti dalla formula di Leibniz.
Non bisogna tuttavia pensare che ciò costituisca un problema per un matematico. Per la sua mentalità, è sufficiente che il metodo proposto, facendo uso di una formula possibilmente elegante, garantisca di trovare quante cifre decimali si vogliano di p. Che poi occorrano milioni di termini per avvicinarsi lentamente ai risultati desiderati è un fatto del tutto secondario e marginale!
Del resto il problema dei calcoli, al giorno d'oggi, è effettivamente diventato secondario. Disponiamo ormai di super calcolatori che riescono a fare milioni di operazioni al secondo. E' perciò possibile ottenere migliaia di cifre esatte di p, anche se poi resta da chiedersi a cosa potranno servire.
 
A proposito di computer, vorrei proporre un giochino, che richiede di ripetere molte volte alcuni semplici calcoli. A farli manualmente ci vorrebbe un bel po' di tempo e di fatica. Un computer è invece in grado di farli al nostro posto:
  1. prediamo due numeri a caso, compresi tra 0 - 1 ((1)) .
  2. eleviamo i due numeri al quadrato e sommiamoli.
  3. se la somma è minore o uguale ad 1, guadagniamo un punto.
  4. ripetiamo per migliaia di volte le tre operazioni suddette, tenendo il conto dei punti (G) e delle prove fatte (P).
  5. calcoliamo G/P e moltiplichiamo per 4.
Ad esempio, con i numeri 0,7281 e 0,5933, la somma dei loro quadrati vale 0,8821..., minore di 1, quindi si ottiene un punto. Invece con 0,8541 e 0,7355 la somma dei quadrati vale 1,2704..., maggiore di 1 e non si ottiene alcun punto.
Se la procedura è stata eseguita correttamente e sopratutto se il numero di prove è stato sufficientemente elevato, il risultato ottenuto al punto 5) non dovrebbe discostarsi molto dal nostro pi greco.
Chi avrebbe mai detto che pi-greco potesse scaturire da due numeri scelti a caso?
E' il frutto del cosiddetto Metodo Montecarlo, ipotizzato da E.Fermi (senza usare tale denominazione) e poi usato da Stanislaw Ulam per risolvere problemi connessi alla diffusione dei neutroni. Chi volesse saperne di più potrà consultare in questo stesso sito l'articolo su Metodo Montecarlo, in particolare il § 23
 
Chi non avesse voglia o non fosse in grado di usare il computer, potrà utilizzare una comune calcolatrice, di quelle che si distribuiscono in omaggio con le scatole di detersivo, per avere con facilità un bel numero di cifre esatte di p.
Il sottoscritto, dopo qualche tentativo con un foglio di calcolo, ha trovato (ma quasi certamente ci sarà qualcun altro che c'è già arrivato prima(2) ) un semplice rapporto, che fornisce le prime 7 cifre decimali di p, con un piccolissimo errore :
 
355/113

Usando la suddetta calcolatrice, si potrà dividere il numeratore per il denominatore e si vedrà apparire sul visore: 3.1415929
Il valore noto delle prime 8 cifre di p è 3.1415926. L'errore è minore di 3 decimilionesimi.

Vittorio De Petris

1Un cronometro digitale può fornire due cifre decimali, leggendo i centesimi di secondo dopo aver premuto il pulsante stop a caso, oppure si possono leggere le tre cifre centrali delle targhe nei veicoli di passaggio, o pescando una carta a caso da ciascuno dei quattro mazzetti di 10 carte ciascuno (dall'asso al re, che vale zero) e componendo con esse un numero decimale di 4 cifre. Il computer può fornire direttamente tali numeri, detti RANDOM, attivando la relativa funzione, che nel più diffuso foglio di calcolo ha la formula =CASUALE().

2Giuliano Bianco mi ha inviato una e-mail, il 9 nov 2003, in cui m'informa che sono stato preceduto da Tsu Ch'ung-Chih, astronomo cinese del V secolo D.C. (notizia presa da M. Gardner "Enigmi e giochi matematici" volume III.)