|
Il metodo MONTE CARLO per l'analisi di un solitario
Andrea Pompili ( anpompil@tin.it)
Monte Carlo è un metodo di indagine statistica per ottenere stime di probabilità in base al conteggio delle frequenze dei vari esiti possibili di un evento rispetto al numero di osservazioni dell'evento stesso; quante più osservazioni sono effettuate, tanto più le stime sono attendibili.
Montecarlo è anche il nome che ho dato a un solitario di carte di pura fortuna e dalle regole talmente semplici che sono sicuro di non averlo inventato per primo.
Da un mazzo di napoletane si gira una carta alla volta, contando a partire da 1 e mantenendo l'ordine iniziale nelle carte girate. Quando il valore di una carta girata (asso = 1) coincide con il numero del conteggio progressivo, la carta va nel monte punti, le carte girate in precedenza tornano in coda al mazzo nello stesso ordine che avevano all'inizio ed il conteggio riparte da 1.
Se il conteggio arriva a 10 senza alcuna carta uguale al numero progressivo, le 10 carte sono eliminate ed il conteggio riprende da 1 usando le carte residue. Si procede fino ad esaurimento del mazzo; al termine il punteggio è la somma dei valori delle carte nel monte punti.
A questo punto si possono formulare diversi quesiti, del tipo:
- qual è il punteggio più probabile?
- quale il più alto possibile?
- quante sono le probabilità di fare almeno un tot punti?
In particolare mi sono riproposto di trovare la terza risposta dopo il seguente episodio.
Un giorno di pioggia in un rifugio, un amico mi osserva giocare a questo passatempo (di ciò si tratta più che di un solitario). Dopo qualche tentativo, totalizzo il discreto punteggio di 83.
"Beh, non è tanto" dice Piero, "fai provare a me, ti supero, magari di un punto!"
"Guarda che è un punteggio alto, non è frequente. Comunque prova"
Al primo tentativo lui fa 84!
In quel momento mi riprometto di dimostrargli quanta fortuna abbia avuto.
In seguito ho quindi messo a punto un programma per PC che gioca il solitario al ritmo di circa 30.000 tentativi al secondo, utilizzando ad ogni tentativo una sequenza casuale di 40 numeri tra 1 e 10 che simula un mazzo di carte napoletane ogni volta rimescolate.
Analizzando le frequenze dei vari risultati su un milione di tentativi, ho constatato che per superare 83 occorrono mediamente 200 tentativi (4.748 volte su un milione si fa più di 83, meno di 5 volte su 1000); il punteggio di 84 lo si ottiene all'incirca ogni 2.500 tentativi (395 volte su un milione). Erano queste le risposte che cercavo per poterle girare all'amico Piero.
Ho poi proseguito nell'indagine: nel grafico qui sotto, che illustra la distribuzione dei risultati, si notano dei picchi di frequenza per i punteggi 0, 10, 20, 30; in assenza dei picchi il risultato più frequente sarebbe il 17. Qual è il motivo dei picchi per i multipli di 10?
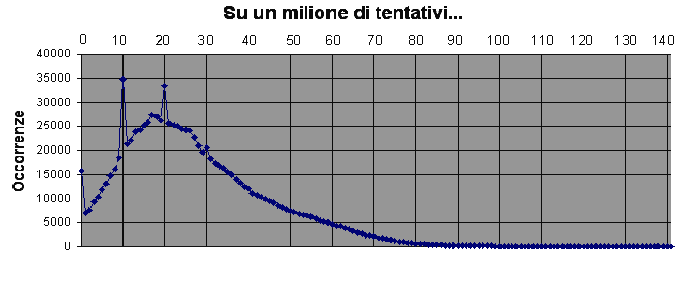
Alla ricerca del punteggio più alto ho ripetuto l'operazione facendo eseguire al programma, in diverse occasioni, un miliardo di tentativi (10 ore di elaborazione). Qui sotto c'è il grafico della prima ricerca da un miliardo, in cui il punteggio più alto realizzato è stato 189.
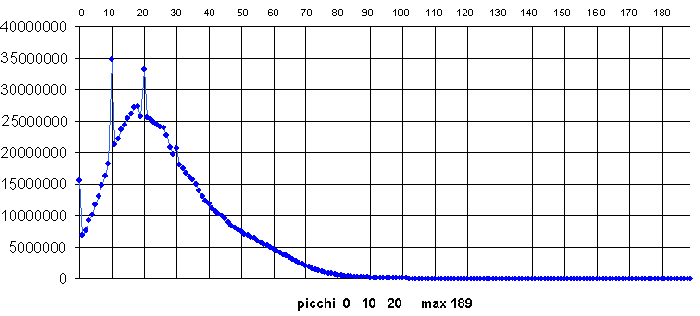
Ho continuato a lanciare il programma a più riprese, ogni volta effettuando 1 o 2 miliardi di tentativi. Il punteggio più alto in assoluto trovato finora in questo modo è 198; qui sotto sono riportate le 3 serie che hanno generato più punti in quella occasione, su 2 miliardi di tentativi.
Tentativo 177.348.748 : punteggio = 198 con 36 carte
mazzo = 1 4 1 9 7 9 5 8 7 9 3 6 5 10 2 3 7 6 9 10 6 1 4 3 8 6 5 8 10 5 2 4 4 10 2 8 7 2 3 1
Tentativo 817.935.424 : punteggio = 196 con 34 carte
mazzo = 1 2 6 7 2 8 3 7 5 3 4 1 9 9 4 3 2 10 9 7 10 1 10 7 4 8 6 8 6 8 10 1 4 5 9 3 2 6 5 5
Tentativo 1.835.888.622 : punteggio = 191 con 33 carte
mazzo = 1 3 3 9 4 8 9 6 1 4 8 6 8 7 5 6 5 9 6 5 10 10 7 5 3 2 4 8 1 9 2 1 7 2 4 10 3 2 10 7
La tabella appresso contiene altri dati relativi alla stessa occasione: sono confermati i picchi relativi a 0, 10, 20; senza i picchi il 18 sarebbe il punteggio più frequente (poco più del 17).
| Punteggi bassi | Punteggi alti | Singole carte
| 0 = 31256224
1 = 13877096
2 = 15270845
3 = 18489274
4 = 20356076
5 = 23598855
6 = 26226389
7 = 29709466
8 = 32696797
9 = 36624311
10 = 69756046
11 = 42582144
12 = 44510646
13 = 47326313
14 = 48820425
15 = 50801229
16 = 52297802
17 = 54523331
18 = 54590909
19 = 51553825
20 = 66595130
21 = 51249992
22 = 50523516
23 = 49593895
. . . . . . . . . . . . . . . . .
| . . . . . . . . . . . . . .
175 = 32
176 = 24
177 = 18
178 = 21
179 = 10
180 = 10
181 = 5
182 = 6
183 = 6
184 = 2
185 = 1
186 = 7
187 = 3
188 = 4
189 = 1
191 = 1
196 = 1
198 = 1
| Carta = 1 : 1803854091 volte
Carta = 2 : 1637505560 volte
Carta = 3 : 1483412365 volte
Carta = 4 : 1338983167 volte
Carta = 5 : 1202873545 volte
Carta = 6 : 1074419914 volte
Carta = 7 : 954898793 volte
Carta = 8 : 846297959 volte
Carta = 9 : 750438484 volte
Carta = 10 : 667597940 volte |
Cercando di capire quanti altri tentativi da uno o due miliardi alla volta avrei dovuto effettuare per trovare il punteggio massimo, ho presto realizzato che non ne sarei venuto a capo.
Infatti, come indica la tabella seguente, le possibili disposizioni indipendenti dal seme in un mazzo di carte napoletane sono date da 40!/4!10, ovvero un numero di 35 cifre: (1,286864E+34), decisamente troppo per un solo PC; e per le carte francesi le cifre necessarie salgono a 50: servirebbe un calcolo distribuito su una rete di potenti elaboratori.
Nella tabella sono indicati anche altri tipi di mazzo variabili per numero di semi e carte per seme, compresi i casi limite di mazzi di due carte (due assi oppure un asso e un due).
Per ogni tipo di mazzo sono indicate le combinazioni possibili, i punti in gioco ed il punteggio massimo realizzabile, se noto.
| C carte
| S semi
| Carte per seme
C / S
| DISPOSIZIONI
C! / (S!c/s)
| punti in gioco
| massimo punteggio |
|---|
| 2
| 2
| 1
| 1
| 2
| 2 |
| 2
| 1
| 2
| 2
| 3
| 1 |
| 3
| 1
| 3
| 6
| 6
| 3 |
| 4
| 2
| 2
| 6
| 6
| 4 |
| 6
| 3
| 2
| 20
| 9
| 7 |
| 4
| 1
| 4
| 24
| 10
| 6 |
| 8
| 4
| 2
| 70
| 12
| 10 |
| 6
| 2
| 3
| 90
| 12
| 9 |
| 10
| 5
| 2
| 252
| 15
| 13 |
| 12
| 6
| 2
| 924
| 18
| 16 |
| 8
| 2
| 4
| 2.520
| 20
| 17 |
| 16
| 8
| 2
| 12.870
| 24
| 22 |
| 12
| 4
| 3
| 34.650
| 24
| 22 |
| 10
| 2
| 5
| 113.400
| 30
| 27 |
| 12
| 3
| 4
| 369.600
| 30
| 28 |
| 15
| 5
| 3
| 756.756
| 30
| 28 |
| 10
| 1
| 10
| 3.628.800
| 55
| 39 |
| 12
| 2
| 6
| 7.484.400
| 42
| 40 |
| 16
| 4
| 4
| 63.063.000
| 40
| 38 |
| 15
| 3
| 5
| 168.168.000
| 45
| 43 |
| 20
| 5
| 4
| 11.732.745.024
| 50 |
| | 16
| 2
| 8
| 81.729.648.000
| 72 |
| | 20
| 4
| 5
| 305.540.235.000
| 60
| 58 ? |
| 20
| 2
|
10
| 2,375881E+15
| 110
|
| | 24
| 4
| 6
| 3,246671E+15
| 84
| |
| 28
| 4
| 7
| 6,647558E+19
| 112
|
| | 40
| 10
| 4
| 4,705361E+21
| 100
|
| | 32
| 4
| 8
| 2,390462E+24
| 144
|
| | 30
| 3
| 10
| 4,386797E+24
| 165
|
| | 36
| 4
| 9
| 1,408102E+29
| 180
|
| | 40
| 4
| 10
| 1,286864E+34
| 220
| 218 ? |
| 40
| 1
| 40
| 8,159153E+47
| 820
|
| | 52
| 4
| 13
| 9,202424E+49
| 364
|
| | 52
| 1
| 52
| 8,065818E+67
| 1378
| |
Spesso il punteggio massimo è dato dalla somma dei punti in gioco meno 2: per le carte napoletane è ipotizzabile che il punteggio più alto possibile sia 218.
Adattando il programma, sono passato ad analizzare mazzi di carte ridotti, e posso dire di avere il quadro abbastanza completo per quei tipi di mazzo in cui il numero di possibili sequenze diverse è inferiore al miliardo.
Nella tabella qui sotto sono riportate tutte le sequenze (o quasi, qualcuna potrebbe essere sfuggita) che generano il punteggio massimo (43) in un ipotetico mazzo composto di quindici carte, 3 semi e 5 carte per seme dall'asso al cinque.
Si tratta di 57 serie vincenti, molte delle quali trovate anche più di una volta: il programma infatti ha effettuato 1 miliardo di tentativi, generando in modo casuale altrettante sequenze diverse, mentre per questo tipo di mazzo le possibili disposizioni sono 168.168.000.
| 1 2 5 4 3 5 2 1 5 4 3 2 3 1 4
| 3 1 3 2 4 3 4 1 2 4 5 5 2 1 5
| 4 1 2 1 5 5 5 3 2 3 1 4 2 4 3 |
| 1 2 5 4 4 3 2 2 1 5 3 5 3 1 4
| 3 1 3 2 4 4 1 5 2 5 5 4 2 1 3
| 4 1 3 2 1 5 5 5 2 3 1 4 2 4 3 |
| 1 3 4 2 4 2 4 2 1 5 5 5 3 3 1
| 3 2 4 1 3 2 1 5 4 5 3 1 4 2 5
| 4 1 3 2 5 5 2 5 4 3 3 2 1 1 4 |
| 1 3 4 2 4 2 4 3 2 1 5 5 5 3 1
| 3 4 1 4 2 1 3 5 2 5 3 1 4 2 5
| 4 1 4 4 2 1 3 3 2 5 3 1 2 5 5 |
| 1 3 5 2 4 4 3 2 1 5 5 2 4 3 1
| 3 4 1 4 2 1 5 4 5 2 3 1 3 2 5
| 4 1 5 4 2 1 3 3 2 5 3 1 4 2 5 |
| 1 4 3 2 1 5 5 4 1 2 5 4 3 3 2
| 3 4 2 4 1 2 4 2 1 5 5 5 3 3 1
| 4 2 4 1 3 2 4 2 1 5 5 5 3 3 1 |
| 2 1 3 2 1 5 4 4 3 5 4 2 1 3 5
| 3 4 2 4 1 2 4 3 2 1 5 5 5 3 1
| 4 2 4 1 3 2 4 3 2 1 5 5 5 3 1 |
| 2 1 3 5 1 5 2 5 4 3 1 4 2 4 3
| 3 4 2 4 2 4 2 1 5 1 5 5 3 3 1
| 4 3 2 1 5 1 5 4 1 2 5 4 3 3 2 |
| 2 1 4 3 5 2 1 5 3 5 3 1 4 4 2
| 3 4 2 4 2 4 2 1 5 5 5 3 1 3 1
| 4 3 2 1 5 5 4 1 2 5 4 3 3 1 2 |
| 2 1 5 1 5 5 1 2 4 4 3 3 2 4 3
| 3 4 2 4 2 4 3 1 2 1 5 5 5 3 1
| 4 4 1 2 5 4 2 2 1 3 5 5 3 3 1 |
| 2 1 5 4 3 3 1 4 4 3 1 2 5 2 5
| 3 4 2 4 2 4 3 2 1 5 5 5 1 3 1
| 4 4 3 2 4 2 1 5 5 1 3 5 2 3 1 |
| 2 3 1 4 2 1 5 3 5 3 1 4 2 5 4
| 3 5 1 3 5 2 4 3 2 4 4 1 5 2 1
| 4 4 3 2 4 3 2 1 5 1 5 5 2 3 1 |
| 2 4 1 4 2 1 3 5 5 3 3 1 2 4 5
| 3 5 2 4 1 4 3 2 1 5 5 2 4 3 1
| 2>5 1 2 4 4 3 2 1 5 5 2 4 3 1 3 |
| 2 4 2 1 5 5 5 1 4 3 3 1 4 3 2
| 3 5 2 4 4 3 2 1 5 1 5 2 4 3 1
| 5 1 3 2 4 3 4 1 5 2 5 4 3 2 1 |
| 2 4 5 4 1 2 3 3 3 1 4 2 5 5 1
|
| 5 1 4 3 5 2 1 5 4 3 2 3 1 4 2 |
| 2 5 4 3 5 1 2 1 5 4 3 2 3 1 4
|
| 5 1 4 4 3 2 2 1 5 3 5 3 1 4 2 |
| 2 5 4 3 5 2 1 5 4 1 3 2 3 1 4
|
| 5 3 2 1 5 5 4 3 3 1 1 4 4 2 2 |
| 2 5 4 3 5 2 1 5 4 3 2 1 3 1 4
|
| 5 3 3 2 1 5 4 4 3 1 1 5 4 2 2 |
| 2 5 4 4 1 3 2 2 1 5 3 5 3 1 4
|
| 5 4 2 4 4 1 3 2 5 3 5 1 3 2 1 |
| 2 5 4 4 2 1 2 1 5 3 5 3 3 1 4
|
| 5 4 3 2 4 1 4 2 5 3 5 1 3 2 1 |
| 2 5 4 4 3 2 1 2 1 5 3 5 3 1 4
|
| 5 5 1 3 5 2 4 3 2 4 3 4 1 2 1 |
| 2 5 4 4 3 2 2 1 5 3 5 1 3 1 4
|
| |
In conclusione, ecco i principali quesiti ancora aperti su Montecarlo e dintorni:
- Qual è il punteggio massimo realizzabile con le carte napoletane? E con quelle francesi?
- Quante sequenze lo generano? Quali?
- Come si spiegano i picchi di frequenza per i multipli di 10?
(A questo proposito un mazzo di carte francesi genera picchi ai multipli di 13 e quello di 15 carte - 3 semi di 5 carte - ai multipli di 5)
- C'è un modo per costruire serie vincenti (senza farle cercare a caso dal programma)?
Chiunque sia in grado di rispondere o di formulare nuove domande è il benvenuto.
Agosto 2002
Andrea Pompili (anpompil@tin.it)
Riferimento bibliografico:
"L'uso del computer nell'insegnamento della Probabilità e della Statistica. Metodo Monte Carlo" Mauro Cerasoli - Vittorio De Petris (http://www.vdepetris.it/Articoli.htm)
|

